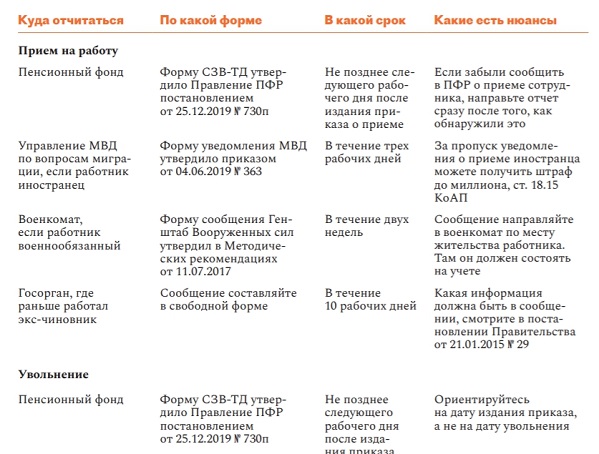
куда сдавать в 2019 году
Одна из форм персонифицированной отчетности – СЗВ-М. Куда сдавать этот отчет? Каков порядок сдачи, если у компании есть удаленно расположенные обособленные подразделения? На эти и другие вопросы ответим в статье.
Голова и обособки
По общему правилу форму нужно сдать в территориальное отделение Пенсионного фонда по месту учета страхователя. Куда сдавать СЗВ-М в 2019 году? В то отделение, где зарегистрирован работодатель.
Под страхователями для целей сдачи данной отчетности понимаются организации и индивидуальные предприниматели, заключившие трудовые и гражданско-правовые договоры с физическими лицами. Если в каком-то месяце компания не ведет деятельность, то это не освобождает ее от необходимости своевременно подать отчет.
С организациями, у которых нет обособленных подразделений все понятно, а куда сдавать СЗВ-М по обособленному подразделению в 2019 году? Если обособка имеет отдельный расчетный счет и начисляет вознаграждения персоналу самостоятельно, то сдавать форму нужно в территориальное отделение Пенсионного фонда по местонахождению такого подразделения.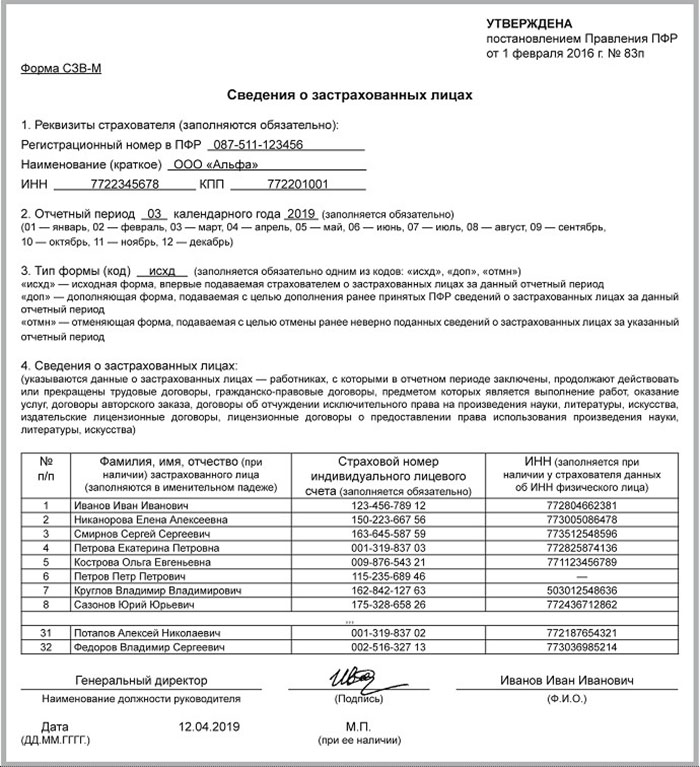
В противном случае, если у обособки нет своего счета, или начисление зарплаты происходит в головном отделении, то данные по сотрудникам такого подразделения нужно включить в общий отчет по головному предприятию. В аналогичном порядке сдается СЗВ-М по подразделениям, находящимся за границей (п. 11, 14 ст. 431 НК РФ, ст. 11 Федерального закона от 15.12.2001 № 167-ФЗ). Теперь вы знаете, куда сдавать отчет СЗВ-М в различных ситуациях.
Бумага или электронка
По закону сведения о физлицах можно сдать в электронной или бумажной форме. Если количество лиц, за которых подается отчет 25 человек и более, то выбора у организации нет. Форма сдается исключительно в электронном виде по формату, утвержденному постановлением Правления ПФР от 07.12.2016 № 1077п (п. 2 ст. 8 Федерального закона от 01.04.1996 № 27-ФЗ).
Сколько бы людей не было поименовано в отчете разбивать его на пачки не нужно. Вне зависимости от количества застрахованных сведения предоставляются одним файлом.
Если число физических лиц не превышает 24 человек, то страхователь может сдать отчет на бумаге. Куда сдавать СЗВ-М? В Пенсионный фонд по месту регистрации. Данные из бухгалтерской программы лучше сохранить на флэшку. Работники Пенсионного фонда могут попросить разнести данные в специальной программе самостоятельно и только после этого примут бумажный носитель.
Новости социальной поддержки
Порядок подачи и рассмотрения электронных обращений граждан
Обращение, направленное на официальный сайт Министерства по электронной почте, должно содержать фамилию, имя, отчество заявителя, почтовый адрес, по которому должен быть направлен ответ, контактный телефон, суть обращения (далее — Интернет-обращение).
Интернет-обращение, поступившее на официальный сайт по электронной почте, распечатывается, и в дальнейшем работа с ним ведется в установленном порядке в соответствии с Федеральным законом от 02.05.2006 г. N 59-ФЗ «О порядке рассмотрения обращений граждан Российской Федерации», административным регламентом предоставления министерством труда и социальной защиты населения Ставропольского края государственной услуги «Организация приема граждан, обеспечение своевременного и полного рассмотрения обращений граждан, принятие по ним решений и направление ответов заявителям в установленный законодательством Российской Федерации срок» (далее — Административный регламент).
Для приема Интернет-обращения заявителя в форме электронного сообщения применяется специализированное программное обеспечение, предусматривающее заполнение заявителем, реквизитов, необходимых для работы с обращениями и для письменного ответа. Адрес электронной почты заявителя (законного представителя) и электронная цифровая подпись являются дополнительной информацией.
Основаниями для отказа в рассмотрении Интернет-обращения, помимо указанных оснований, в пункте 2.9 Административного регламента, также являются:
- отсутствие адреса (почтового или электронного) для ответа;
- поступление дубликата уже принятого электронного сообщения;
- некорректность содержания электронного сообщения.
Ответ заявителю на Интернет-обращение может направляться как в письменной форме, так и в форме электронного сообщения.
Заявителю гарантируется не разглашение без его согласия сведений, содержащихся в Интернет-обращении, а также сведений, касающихся частной жизни гражданина.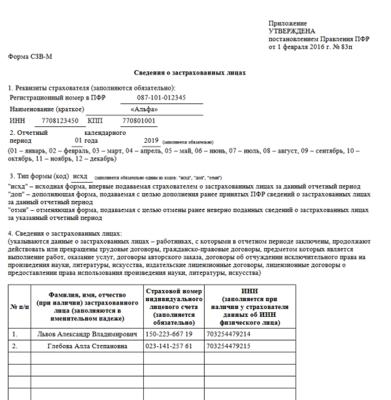 Информация о персональных данных заявителей хранится и обрабатывается с соблюдением требований российского законодательства о персональных данных.
Информация о персональных данных заявителей хранится и обрабатывается с соблюдением требований российского законодательства о персональных данных.
Интернет-обращения представляются руководству Министерства для рассмотрения. На наиболее часто задаваемые вопросы периодически публикуются ответы руководителей Министерства. Ваш вопрос, заданный в Интернет-обращении может быть опубликован на сайте в обезличенной форме.
Бизнес гибнет от бумаг
Предприниматели в России тонут в бумажной отчетности. Ежегодно только одна налоговая запрашивает от бизнесмена от одного до 11 документов. Кроме того, существует до 158 всевозможных форм статистики для разных видов деятельности. А еще отчеты бухгалтерские, пара бумаг для Фонда социального страхования, еще до четырех — для Пенсионного фонда, специальная ведомственная отчетность (например, в органы тарифного регулирования или документы об использовании средств долевого строительства, отчеты частных медицинских организаций в фонды ОМС, декларации об объеме производства и оборота алкогольной продукции и тому подобное).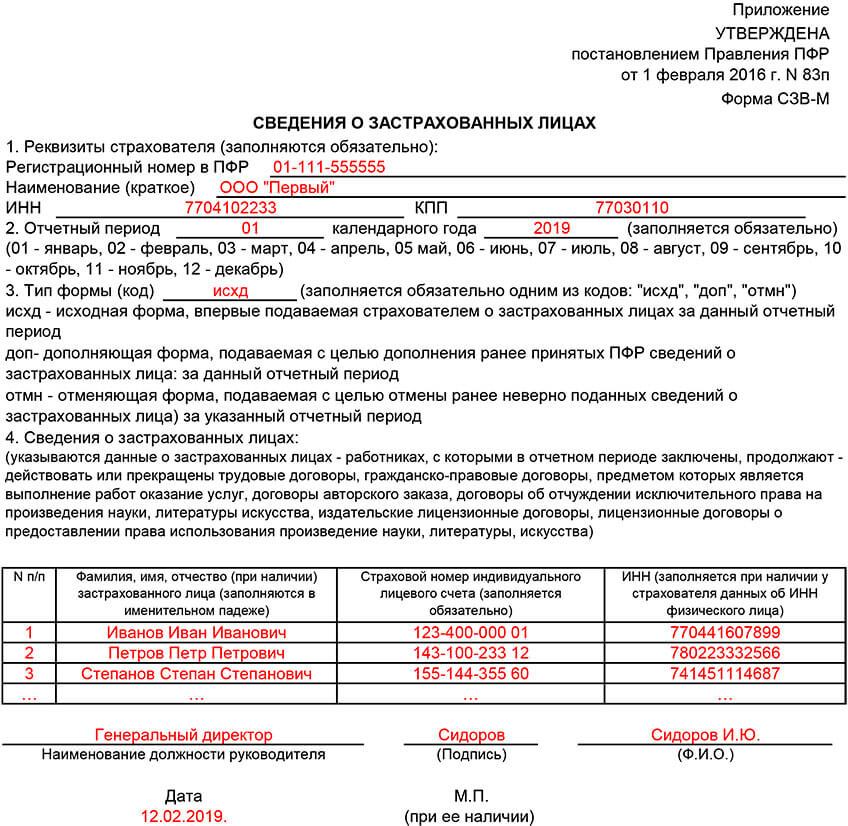
Чем бизнес больше, тем выше стопка документов, которая может доходить до тысячи бумаг в пересчете на одну фирму. При этом табель форм федерального статистического наблюдения на 2020 год содержит более 60 отдельных дат сдачи отчетов. В рамках одного вида деятельности количество дат может доходить до 10 в год, а для многопрофильных предприятий — и того более. Для субъектов МСП рост нагрузки происходит скачкообразно: если микробизнесу требуется заполнять меньше форм, то малому и среднему — в несколько раз больше.
Предприниматели поголовно жалуются на то, что данные различных форм бумаг, предоставляемых с периодичностью ото дня до года, часто дублируют друг друга. Совокупные обязательства представляются избыточными, накладывают административное бремя на отдельные категории предпринимателей, а нарушение сроков сдачи часто несет риски получить существенный административный штраф.
Кстати, в этом году запущена сплошная перепись малого и среднего бизнеса. Хоть и ведется она в электронном формате, согласитесь, ведь тоже дополнительная нагрузка?! Мир уже давно начал уходить от традиционных концепций статистики — вся мировая система переходит на big data.
Элемент такой системы в России — ФНС, которая аккумулирует данные со всей страны с онлайн-касс и получает ежедневную картину потребления и активности малого бизнеса.
Поэтому с целью оптимизации процесса подачи различных видов отчетности представляется возможным создание «единого окна» на базе Федеральной налоговой службы России с обеспечением возможности электронного взаимодействия с предпринимателями и подачей всех документов в одну инстанцию. Для реализации указанного замысла, по мнению специалистов Партии Роста, необходимо:
- создать единый репозиторий отчетных данных на базе ФНС России, куда субъекты предпринимательства будут предоставлять все необходимые формы отчетности; заинтересованные ведомства, региональные и муниципальные органы власти будут получать необходимые данные из репозитория в рамках межведомственного взаимодействия;
- провести полную инвентаризацию форм отчетности и исключить избыточные и дублирующие друг друга формы, определив, таким образом, оптимальный набор отчетности, предоставляемой в репозиторий;
- обеспечить возможность передачи всех видов отчетности субъектами предпринимательства в единый репозиторий в электронном формате.
 На законодательном уровне в ст. 13 и 14 Федерального закона от 27.07.2006 № 149-ФЗ «Об информации, информационных технологиях и о защите информации» установить приоритет программного (посредством API) доступа к порталам сдачи отчетности и иным государственным информационным системам, а также заблаговременной публикации любых изменений в формы и форматы предоставления данных в адрес госорганов.
На законодательном уровне в ст. 13 и 14 Федерального закона от 27.07.2006 № 149-ФЗ «Об информации, информационных технологиях и о защите информации» установить приоритет программного (посредством API) доступа к порталам сдачи отчетности и иным государственным информационным системам, а также заблаговременной публикации любых изменений в формы и форматы предоставления данных в адрес госорганов.
На практике это будет означать начало формирования единой системы big data в России под эгидой государства. Мы уверены, эта система сможет помочь оценивать степень достижения национальных целей и приоритетов, своевременно корректировать программы и перераспределять ресурсы, оценивать состояние секторов экономики. А бизнес сможет сдавать данные в удобном и понятном формате, что снизит административную нагрузку, особенно в непростой постпандемийный период.
Однако все понимают: чтобы реализовать этот достаточно глобальный план, уйдет немало времени. Поэтому в Партии Роста проанализировали и работу существующей системы отчетности.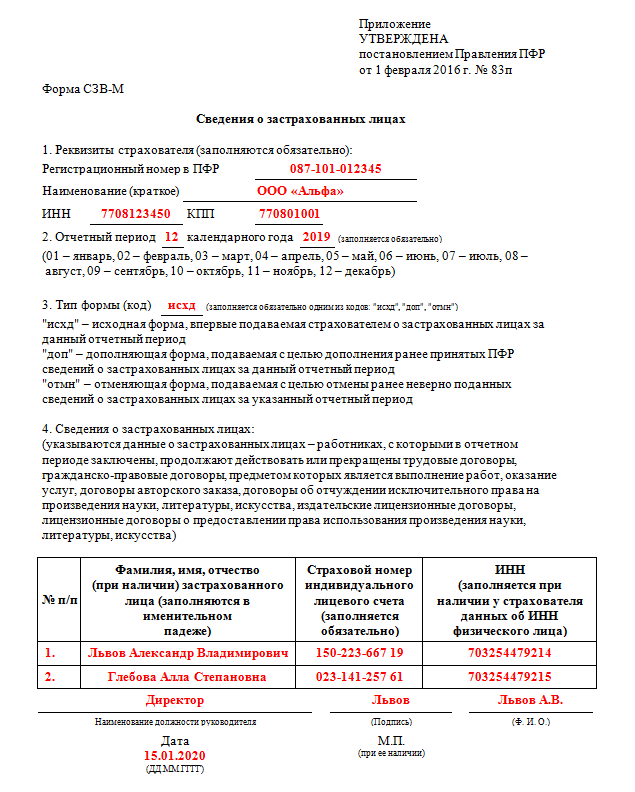 Вот какие точечные меры мы можем предложить.
Вот какие точечные меры мы можем предложить.
В связи с применением онлайн-касс:
- В ежемесячной форме статистического наблюдения Форма П-1 «Сведения о производстве и отгрузке товаров и услуг» исключить сведения по оборотам розничной торговли: Графы 1 и 2 строки 02 раздела 1, Графы 1 и 2 строки 22 Раздела 3, Раздел 5 полностью.
- В ежеквартальной форме статистического наблюдения Форма № 3-ТОРГ (ПМ) «Сведения об обороте розничной торговли малого предприятия» исключить: Графы 1 и 2 строка 01 Раздел 1, Графы 1 и 2 строка 02 Раздел 1, Графы 4 и 5 строки 66 Раздел 2.
- В годовой форме статистического наблюдения Форма 1-ТОРГ «Сведения о продаже товаров организациями оптовой и розничной торговли»: Раздел 2 исключить, Раздел 3 столбец 5 исключить, Графу 5 Раздел 4 полностью исключить.
- Провести анализ возможности перевода наблюдений в розничной торговле и услугах населению на межведомственный обмен данными (в связи с введением онлайн-касс).
- Годовая форма статистического наблюдения Форма № 12-Ф «Сведения об использовании денежных средств» дублирует годовую форму «Отчет о движении денежных средств» к годовому балансу.
 Предлагаем по итогам 2020 года наладить обмен информацией между Росстатом и ФНС России для заполнения формы 12-Ф.
Предлагаем по итогам 2020 года наладить обмен информацией между Росстатом и ФНС России для заполнения формы 12-Ф. - Провести аудит требований по предоставлению форм отчетности по социальным платежам с проработкой вопросов объединения ряда форм (например, объединить отчеты СЗВ-М и СЗВ-ТД, объединить «Расчет по страховым взносам» и СЗВ-СТАЖ). В таком случае для ежемесячной формы статистического наблюдения Форма № П-4 (НЗ) «Сведения о неполной занятости и движении работников» можно будет брать данные из объединенного отчета «Расчет по страховым взносам» и СЗВ-СТАЖ. В форме ФСС-4 упразднить данные, дублирующие сведения расчетов по страховым взносам.
- Объединить ежемесячные, квартальные, полугодовые и годовые статистические отчеты П-4 «Сведения о численности и заработной плате работников» в один ежемесячный, но с разбивкой по ОКПО.
- Рассмотреть возможность упразднения месячного статистического отчета № П-3 «Сведения о финансовом состоянии организации» с получением данных для статистических целей из баз данных ФНС России.

- На законодательном уровне установить обязательность заблаговременной публикации любых изменений в формы и форматы предоставления отчетных данных в адрес госорганов.
- Определить периодичность предоставления отчетности для всех субъектов МСП для любых наблюдений — не чаще 1 раза в квартал.
- Установить единые даты сдачи статистической отчетности вне зависимости от отрасли.
- Установить пятилетний «мораторий» на подачу отчетности ИП и ЮЛ с численностью менее 15 человек в случае, если они участвовали в сплошном наблюдении.
- Запретить органам статистического наблюдения на практике требовать формы налоговой отчетности у субъектов предпринимательства.
- Провести аудит установленных в КОАП размеров штрафов за непредставление первичных статистических данных и иных видов отчетности и проработать вопрос их снижения в проекте нового кодекса по административным правонарушениям.
- Провести анализ возможности интеграции форм статистического наблюдения, в том числе создание единых форм с приведением отраслевых показателей в приложениях к основной форме статистического наблюдения.

Подписывайтесь на канал «Инвест-Форсайта» в «Яндекс.Дзене»
Заполнить сведения о застрахованных лицах
Заполнить сведения о застрахованных лицахВсе организации и индивидуальные предприниматели должны сдавать отчетность в Пенсионный фонд по форме «СЗВ-М». Если численность сотрудников более 25 человек, отчет представляется только в электронном виде.
Срок сдачи
Сведения подаются ежемесячно не позднее 15 числа месяца, следующего за отчетным периодом.
Ответственность за несданную отчетность
Как сформировать
- В разделе «Отчетность/Пенсионный» или «Учет/Отчетность/Пенсионный» (в зависимости от конфигурации) создайте отчет «СЗВ-М Сведения о застрахованных лицах».
- Проверьте, правильно ли указан получатель и реквизиты организации.
- Перейдите в раздел «Сотрудники», нажмите «+ Сотрудник» и добавьте работников.
- Заполните СНИЛС и ИНН сотрудников.
- Проверьте отчет и отправьте его в ПФ.

Отчет будет принят, когда пенсионный фонд пришлет положительный протокол.
Лицензия
Любой тариф сервиса «Отчетность через интернет».
- В разделе «ПФР» создайте новый отчет и выберите форму «СЗВ-М Сведения о застрахованных лицах».
- Проверьте отчетный период, представителя в ПФР и нажмите «Далее».
- На вкладке «Отредактировать отчет» нажмите «Сведения о застрахованных лицах».
- В открывшемся окне кликните «Добавить» и выберите сотрудников.
- Проверьте СНИЛС и ИНН работников. Если они не указаны, выделите строку с ФИО сотрудника, нажмите «Изменить» и заполните сведения.
- Когда все сведения будут заполнены, проверьте и отправьте отчет.
Отчет будет принят, когда пенсионный фонд пришлет положительный протокол.
Лицензия
Любой тариф сервиса «Отчетность через интернет».
- В разделе «Пенсионный» создайте отчет и выберите форму «СЗВ-М Сведения о застрахованных лицах».
- Нажмите «Сведения о застрахованных лицах».

- В открывшемся окне кликните «Добавить» и выберите сотрудников.
- Убедитесь, что у каждого работника указаны СНИЛС и ИНН работников. Если нет, откройте сведения о сотруднике и заполните их.
- В разделе «Реквизиты» проверьте данные организации, получателя и подписанта.
- Когда все сведения будут заполнены, проверьте и отправьте отчет.
Отчет будет принят, когда пенсионный фонд пришлет положительный протокол.
Лицензия
Любой тариф сервиса «Отчетность через интернет».
Как сдать отчет по форме СЗВ-М?
Получать статьи на почту
Подключите сервис 1С-Отчетность бесплатно на 30 дней!
Шаг 1. Открытие раздела Документы персучета
В программе 1С заходим во вкладку Отчетность, справки и выбираем Документы персучета.
Рис. 1. Вкладка Отчетность, справки в 1С: ЗУП ред. 3.1
Шаг 2. Создание отчета по форме СЗВ-М
В отрывшемся разделе Документы персучета нажимаем на кнопку Создать и выбираем Сведения о застрахованных лицах, СЗВ-М.
Рис. 2. Раздел Документы персучета
Шаг 3. Заполнение отчета по форме СЗВ-М
В отчете выбираем отчетный период и тип формы «Исходная». Нажимаем кнопку Заполнить.
Рис. 3. Заполнение отчета о застрахованных лицах
Шаг 4. Проверка корректности заполнения отчета
Сервис позволяет запустить программу, проверяющую корректность заполнения отчета.
На кнопке Отправить нажмите на стрелку вниз и выберите Проверить в Интернете.
Рис. 4. Проверка корректности заполнения отчета
В открывшемся окне заполните согласие на передачу персональных данных и нажмите Продолжить.
Рис. 5. Форма согласия на передачу персональных данных
По итогам проверки отчета программа выдаст сообщение. Если ошибок в отчете не обнаружено, переходите к следующему шагу.
Рис. 6. Сообщение об отсутствии ошибок в отчете
Шаг 5. Отправка отчета в Пенсионный фонд РФ
На кнопке Отправить нажмите на стрелку вниз и выберите Отправить в ПФР.
Рис. 7. Отправка отчета в ПФР
Подтвердите, что отчет заполнен полностью и корректно, нажмите отправить.
Рис. 8. Подтверждение отправки отчета
Далее вы увидите сообщение о том, что отчет успешно отправлен в ПФР.
Рис. 9. Сообщение о сдаче отчета
Шаг 6. Проверка отправки отчета
Для того чтобы проверить отправку отчета в разделе Отчетность, справки, зайдите в раздел 1С-Отчетность.
Рис. 10. Вкладка Отчетность, справки в 1С: ЗУП ред. 3.1
В разделе Отчеты можно увидеть отправленные в контролирующие органы документы и их статус. Отчет по форме СЗВ-М сразу после отправки будет иметь статус Отправлено в ПФР.
Рис. 11. Вкладка Отчеты в разделе 1С-Отчетность
После обновления информации с контролирующими органами статус отчета должен измениться на Отчет успешно сдан.
С сервисом 1С-Отчетность сдать отчет просто и удобно. Вы можете оформить у нас бесплатный доступ на месяц к сервису, для того чтобы попробовать в работе все преимущества.
Подключите сервис бесплатно на 30 дней!
Ответы на часто возникающие вопросы
Когда сдавать отчет
Отчет о застрахованных лицах необходимо сдавать до 15-го числа месяца, следующего за отчетным.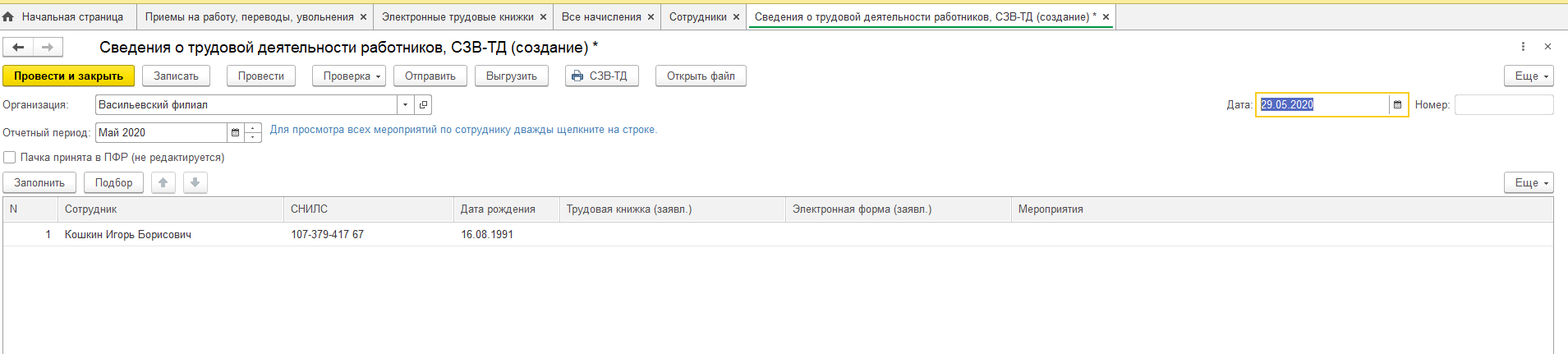
Кому нужно сдавать отчет
Всем организациям и ИП, имеющим в найме сотрудников по трудовому и гражданско-правовому договору, необходимо подавать в ПФР сведения о застрахованных лицах.
В отчет должны включаться сотрудники в декрете, отпуске и уволившиеся в рамках отчетного периода.
Можно ли сдавать отчет досрочно
Отчет можно сдать с 1-го числа месяца, следующего за отчетным.
Как исправить ошибку в отчете
Чтобы исправить ошибку в сведениях отчета по форме СЗВ-М, необходимо заполнить и отправить дополняющую/отменяющую форму.
Остались вопросы?
Наши специалисты свяжутся с вами, чтобы уточнить подробности!
Использование машины опорных векторов для улучшения диагностики неисправностей коробок передач
Коробки передач — это механические устройства, которые играют важную роль в нескольких приложениях, например, в трансмиссии автомобилей. Их неисправность может привести, в частности, к экономическим потерям и несчастным случаям. Появление мощных графических процессоров позволяет использовать решения на основе глубокого обучения для решения многих проблем, включая диагностику неисправностей редукторов. Эти решения обычно требуют значительного объема данных, высокой вычислительной мощности и длительного процесса обучения.Обучение систем на основе глубокого обучения может оказаться невозможным, если графические процессоры недоступны. В этой статье предлагается решение для сокращения времени обучения систем диагностики неисправностей на основе глубокого обучения без ущерба для их точности. Решение основано на использовании этапа принятия решения для интерпретации всех вероятностных выходов классификатора, выходной слой которого имеет функцию активации softmax. Для принятия решения применялись два алгоритма классификации. Мы сократили время обучения почти на 80% без ущерба для средней точности системы диагностики неисправностей.
Их неисправность может привести, в частности, к экономическим потерям и несчастным случаям. Появление мощных графических процессоров позволяет использовать решения на основе глубокого обучения для решения многих проблем, включая диагностику неисправностей редукторов. Эти решения обычно требуют значительного объема данных, высокой вычислительной мощности и длительного процесса обучения.Обучение систем на основе глубокого обучения может оказаться невозможным, если графические процессоры недоступны. В этой статье предлагается решение для сокращения времени обучения систем диагностики неисправностей на основе глубокого обучения без ущерба для их точности. Решение основано на использовании этапа принятия решения для интерпретации всех вероятностных выходов классификатора, выходной слой которого имеет функцию активации softmax. Для принятия решения применялись два алгоритма классификации. Мы сократили время обучения почти на 80% без ущерба для средней точности системы диагностики неисправностей.
1. Введение
Редукторы — это механические устройства, которые обеспечивают преобразование скорости и крутящего момента от вращающихся источников энергии в другие механизмы. Они играют решающую роль в нескольких приложениях, например, в промышленных вращающихся машинах, автомобилях и ветряных турбинах. Их неисправность может не только нарушить работу данной системы, но также привести к экономическим потерям и рискам безопасности [1]. Таким образом, использование быстрых и эффективных методов диагностики неисправностей необходимо, поскольку раннее обнаружение отказов позволяет более эффективно управлять действиями по техническому обслуживанию и приводит к более безопасной работе системы [2].
Коробки передач могут иметь несколько режимов отказа. Большинство из них связано с механическими компонентами и условиями смазки. Одним из видов отказа, требующим внимания, является поломка зубьев шестерен, которая может значительно нарушить работу машины [3].
Благодаря появлению мощных вычислительных устройств, например, графических процессоров (GPU), методы глубокого обучения стали важными инструментами в областях исследования обнаружения и диагностики неисправностей. Их превосходная производительность в приложениях, связанных с задачами классификации и обнаружения объектов, также способствовала их популяризации [4].
Их превосходная производительность в приложениях, связанных с задачами классификации и обнаружения объектов, также способствовала их популяризации [4].
В последние годы появилось множество работ, связанных с глубоким обучением и диагностикой неисправностей в коробках передач. Zhao et al. [5] предложили вариант глубоких остаточных сетей (DRN), который использует динамически взвешенные вейвлет-коэффициенты для улучшения производительности диагностического процесса. Их работа основана на отсутствии единого мнения о наиболее критических полосах частот относительно полезной информации для систем, выполняющих диагностику планетарных коробок передач.Их система находит отличительные наборы характеристик, динамически регулируя веса, применяемые к коэффициентам вейвлет-пакетов. Cabrera et al. [6] предложили использовать глубокую сверточную нейронную сеть (DCNN), обученную на усовершенствованном многослойном сверточном автокодировщике (SCAE), для определения серьезности неисправности в коробках передач. Их система выполняет неконтролируемое обнаружение иерархических частотно-временных шаблонов с помощью DCNN. SCAE улучшает производительность DCNN за счет фиксации априорных шаблонов.
Их система выполняет неконтролируемое обнаружение иерархических частотно-временных шаблонов с помощью DCNN. SCAE улучшает производительность DCNN за счет фиксации априорных шаблонов.
Кроме того, Дойч и Хе [7] используют прямую сеть глубоких убеждений (DBN) для прогнозирования оставшегося срока службы механических машин.Они сочетают в себе возможности самообучения по функциям DBN с предсказательной силой нейронных сетей с прямой связью для извлечения характеристик из сигналов вибрации, оценки целостности машины и выполнения прогнозов. Jiang et al. [8] предложили использовать многоуровневые автокодеры с шумоподавлением для диагностики неисправностей редукторов ветряных турбин. Функции изучаются в процессе неконтролируемого процесса, за которым следует контролируемый процесс точной настройки с информацией о метках для классификации.Они также используют несколько уровней шума для обучения автокодировщика и расширения возможностей изучения и классификации функций. Jiang et al. [9] также предложили систему диагностики коробки передач, основанную на многомасштабных сверточных нейронных сетях. Они объединили многомасштабное и иерархическое обучение для сбора информации в разных масштабах, улучшив производительность классификатора.
Они объединили многомасштабное и иерархическое обучение для сбора информации в разных масштабах, улучшив производительность классификатора.
Монтейро и др. [10] предложили систему диагностики неисправностей, основанную на спектрограммах преобразования Фурье (FT) и глубоких сверточных нейронных сетях.В своей работе они также обсуждали влияние глубины модели и количества доступных обучающих данных на производительность сети. Shao et al. [11] использовали трансферное обучение для диагностики неисправностей механических машин. Модель DCNN, предварительно обученная в ImageNet, с последующим процессом тонкой настройки, выполнила диагностику неисправностей. В других работах, например, Zeng et al. [12] и Liao et al. [13], используйте сверточные нейронные сети, связанные с S- и вейвлет-преобразованиями, для классификации состояния работоспособности коробки передач соответственно.
Одной из основных проблем, связанных с решениями на основе глубокого обучения для систем диагностики неисправностей, является их вычислительная нагрузка; Например, процесс обучения глубоких моделей часто бывает долгим и требует большого количества обучающих данных. Такая неудача обычно преодолевается с помощью компьютеров с мощными графическими процессорами, например, [12]. Однако такое оборудование не всегда доступно каждому. Таким образом, необходимо найти альтернативные способы снижения вычислительных затрат на решения на основе глубокого обучения без ущерба для их производительности в отношении точности.
Такая неудача обычно преодолевается с помощью компьютеров с мощными графическими процессорами, например, [12]. Однако такое оборудование не всегда доступно каждому. Таким образом, необходимо найти альтернативные способы снижения вычислительных затрат на решения на основе глубокого обучения без ущерба для их производительности в отношении точности.
В этой статье предлагается добавить этап принятия решения в выходные данные систем диагностики неисправностей на основе DCNN, которые обычно основаны на алгоритмах классификации [5, 10, 12, 13]. Выходы этих систем часто представляют вероятность того, что данный вход принадлежит к режиму отказа в данном наборе. Выбирается режим отказа, который представляет наибольшее значение вероятности. Хотя этот подход оказался разумным для ряда приложений, информация, предоставляемая оставшимися выходными данными, обычно теряется.
Мы полагаем, что эта информация также может быть использована для повышения производительности классификатора. Примером является тот, который проанализирован в [6, 7], где ставится проблема диагностики серьезности неисправности, связанной с режимом отказа из-за поломки зуба шестерни. На этапе принятия решения анализируются выходные данные всех классов, то есть уровней серьезности, и определяется серьезность неисправности коробки передач на основе их распределения вероятностей. Поскольку эта уловка улучшает результаты классификации, ту же архитектуру модели можно обучить за меньшее количество эпох без ущерба для ее точности, тем самым сокращая время обучения.С другой стороны, этапы принятия решения — хорошо известные инструменты. Они обычно используются в мультимодальных системах классификации и системах классификации на основе комитетов. Они объединяют результаты, полученные несколькими классификаторами, для повышения точности всей системы [14, 15].
На этапе принятия решения анализируются выходные данные всех классов, то есть уровней серьезности, и определяется серьезность неисправности коробки передач на основе их распределения вероятностей. Поскольку эта уловка улучшает результаты классификации, ту же архитектуру модели можно обучить за меньшее количество эпох без ущерба для ее точности, тем самым сокращая время обучения.С другой стороны, этапы принятия решения — хорошо известные инструменты. Они обычно используются в мультимодальных системах классификации и системах классификации на основе комитетов. Они объединяют результаты, полученные несколькими классификаторами, для повышения точности всей системы [14, 15].
Остальная часть этого документа определяется следующим образом: Раздел 3 представляет детали экспериментов, проведенных в этом исследовании, Раздел 4 представляет полученные результаты и обсуждает их актуальность, а Раздел 5 объясняет основные выводы и последствия этой работы.
2. Теоретические основы
2.
 1. Сверточные нейронные сети
1. Сверточные нейронные сети Сверточные нейронные сети — это модели, вдохновленные биологическими процессами. Схема связей между нейронами, то есть процессорами нейронных сетей, аналогична структуре зрительной коры головного мозга животных. Они хорошо выполняют задачи распознавания и классификации объектов [16]. Обнаружение объектов [17], обнаружение заболеваний [18] и диагностика неисправностей [6, 10] — вот три примера приложений, использующих CNN.Их основная структура состоит из входного слоя, чередующихся блоков сверточных и объединяющих слоев, за которыми следуют полностью связанные слои, и выходного слоя [16]. В зависимости от приложения могут произойти изменения в этой структуре. Эта структура проиллюстрирована на рисунке 1. Роль каждого уровня поясняется следующим образом: (a) Входной уровень: этот уровень получает и хранит необработанные входные данные. Он также определяет ширину, высоту и количество каналов входных данных [19]. (B) Сверточные слои: они изучают представления объектов из набора входных данных и генерируют карты признаков.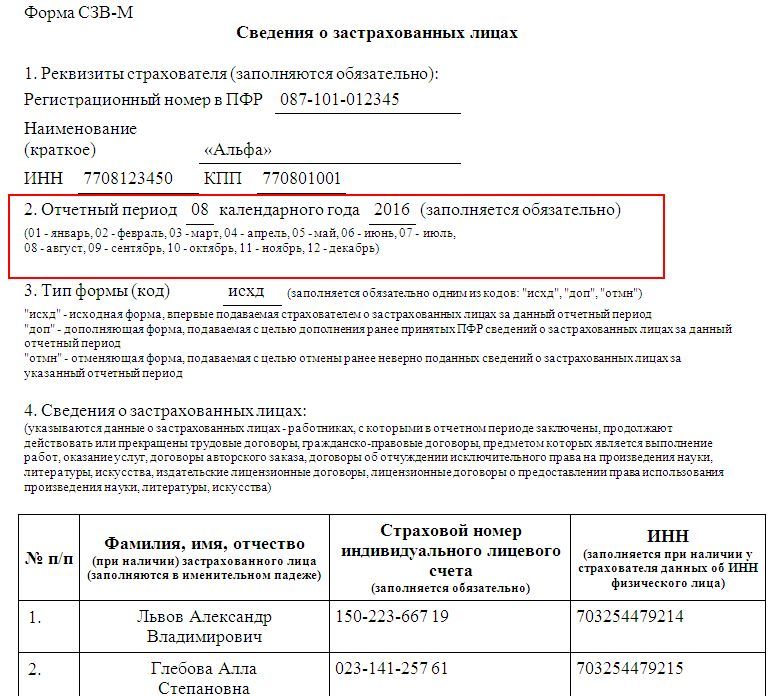 Эти карты создаются путем свертки их входных данных с набором изученных весов. Функция активации, например функция ReLU, применяется к выходу этапа свертки. Следующее уравнение показывает общую формулировку сверточного слоя: в котором l относится к текущему слою, i и j — это индексы элементов предыдущего и текущего слоев, соответственно, это набор входных данных. maps, k — матрица весов сверточного ядра i -го слоя l , примененная к j -й входной карте признаков, а b — смещение.(c) Объединение слоев: они уменьшают пространственное разрешение карт признаков, улучшая пространственную инвариантность к входным искажениям и переносам [19]. В большинстве недавних работ используется разновидность этого уровня, называемая max pooling [16]. На следующие слои распространяется максимальное значение из окрестности элементов. Эта операция определяется тем, что это результат процесса объединения в отношении j -й карты признаков и элемент в местоположении ( p ; q ), содержащийся в области объединения.
Эти карты создаются путем свертки их входных данных с набором изученных весов. Функция активации, например функция ReLU, применяется к выходу этапа свертки. Следующее уравнение показывает общую формулировку сверточного слоя: в котором l относится к текущему слою, i и j — это индексы элементов предыдущего и текущего слоев, соответственно, это набор входных данных. maps, k — матрица весов сверточного ядра i -го слоя l , примененная к j -й входной карте признаков, а b — смещение.(c) Объединение слоев: они уменьшают пространственное разрешение карт признаков, улучшая пространственную инвариантность к входным искажениям и переносам [19]. В большинстве недавних работ используется разновидность этого уровня, называемая max pooling [16]. На следующие слои распространяется максимальное значение из окрестности элементов. Эта операция определяется тем, что это результат процесса объединения в отношении j -й карты признаков и элемент в местоположении ( p ; q ), содержащийся в области объединения. Процесс объединения также известен как субдискретизация [19]. (D) Полностью связанные и выходные уровни: они интерпретируют представления функций и выполняют рассуждения высокого уровня [16]. Они также вычисляют баллы для каждого выходного класса [19]. Количество выходных узлов зависит от количества классов [12].
Процесс объединения также известен как субдискретизация [19]. (D) Полностью связанные и выходные уровни: они интерпретируют представления функций и выполняют рассуждения высокого уровня [16]. Они также вычисляют баллы для каждого выходного класса [19]. Количество выходных узлов зависит от количества классов [12].
2.2. Спектрограммы преобразования Фурье
Преобразование Фурье (FT) — важный метод в области анализа сигналов. Он сообщает частотный состав данного сигнала, а также вклад каждой частоты относительно амплитуды [20].Фильтрация шума, распознавание образов и модуляция сигналов — это некоторые приложения, которые можно улучшить с помощью преобразования Фурье и его вариантов, например, дискретного преобразования Фурье (ДПФ), подходящего для обработки цифровых сигналов, и быстрого преобразования Фурье (БПФ), более эффективный алгоритм вычисления ДПФ [21].
Спектрограммы преобразования Фурье представляют сигналы с использованием информации о времени, частоте и величине. Кратковременное преобразование Фурье (STFT) — это вариант FT, обычно используемый для генерации такого рода представлений, поскольку он выполняет зависящий от времени спектральный анализ [21].Спектрограммы показывают, как спектр частот данного сигнала изменяется во времени. Спектрограммы также используются в приложениях диагностики неисправностей [10, 22].
Кратковременное преобразование Фурье (STFT) — это вариант FT, обычно используемый для генерации такого рода представлений, поскольку он выполняет зависящий от времени спектральный анализ [21].Спектрограммы показывают, как спектр частот данного сигнала изменяется во времени. Спектрограммы также используются в приложениях диагностики неисправностей [10, 22].
2.3. Машины опорных векторов
Машина опорных векторов (SVM) — это универсальный и мощный метод машинного обучения [23]. Его можно использовать для решения задач классификации (как линейной, так и нелинейной), регрессии и даже обнаружения выбросов, что делает его одним из самых популярных алгоритмов машинного обучения [23, 24]. Его использование также популярно при диагностике неисправностей вращающегося оборудования [25].Этот метод направлен на идентификацию гиперплоскостей, способных разделять наборы данных на пространственные объекты большой размерности. Разделение между наборами данных называется маржей, и SVM максимизирует маржу [23].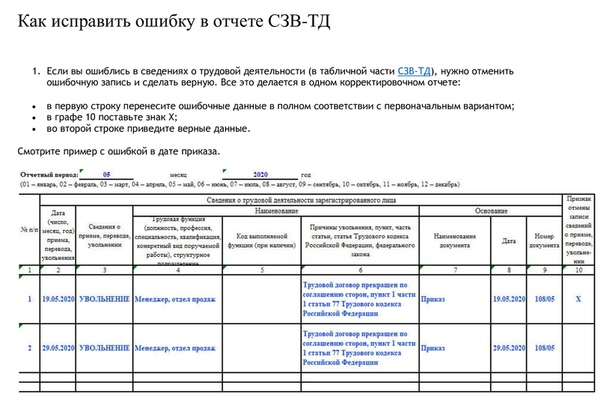
Линейно разделяемый набор данных позволяет SVM определять гиперплоскости, способные разделять данные на категории, независимо от количества измерений, представленных пространством признаков. Однако в большинстве приложений информация не является линейно разделимой в пространствах признаков с заданной размерностью.Таким образом, необходимо сопоставить набор данных с пространством признаков с большим количеством измерений, в котором данные будут линейно разделяемыми. Этот процесс отображения выполняется с использованием ядер, например ядер полиномиальных и радиальных базисных функций [23, 24].
2.4. Многослойный персептрон
Многослойный персептрон (MLP) — это нейронная сеть прямого распространения. MLP могут различать нелинейно разделяемые шаблоны. Эти алгоритмы состоят из нескольких узлов, называемых «нейронами», которые расположены на нескольких уровнях, как ориентированный граф.Каждый слой полностью связан с последующим. Эти слои обычно делятся на три типа: входные, скрытые и выходные. Многослойные персептроны считаются универсальными приближениями. Один MLP скрытого слоя с достаточным количеством нейронов может аппроксимировать любую заданную непрерывную функцию [23, 24].
Многослойные персептроны считаются универсальными приближениями. Один MLP скрытого слоя с достаточным количеством нейронов может аппроксимировать любую заданную непрерывную функцию [23, 24].
3. Материалы и методы
3.1. Экспериментальная установка: получение сигналов вибрации
Мы расположили экспериментальную установку в соответствии с рисунком 2. Она использовалась для получения измерений вибрации редуктора.Электродвигатель (M) приводит в движение коробку передач, состоящую из двух шестерен (Z1 и Z2). Эти шестерни установлены на независимых валах. Магнитный тормоз (B) подключен к выходному валу. В таблице 1 перечислены некоторые особенности этих компонентов.
| ||||||||||||||||
Кроме того, привод скорости Danfoss VLT 1: 5 кВт приводит в движение электродвигатель, а источник напряжения TDK Lambda (GEN 150-10, 0–150 В, 10 А) приводит в действие магнитный тормоз. Однонаправленный акселерометр ( A, ), который был вертикально установлен на коробке передач, рядом с входным валом, собирает сигналы вибрации. Этот акселерометр представляет собой датчик IMI 603C01, 100 мВ / г. Карта сбора данных NI9234 выполняет оцифровку аналоговых сигналов. Эта карта имеет разрешение 24 бита, частоту дискретизации 50 кГц и предназначена для пьезоэлектрических датчиков.
Однонаправленный акселерометр ( A, ), который был вертикально установлен на коробке передач, рядом с входным валом, собирает сигналы вибрации. Этот акселерометр представляет собой датчик IMI 603C01, 100 мВ / г. Карта сбора данных NI9234 выполняет оцифровку аналоговых сигналов. Эта карта имеет разрешение 24 бита, частоту дискретизации 50 кГц и предназначена для пьезоэлектрических датчиков.
Как упоминалось ранее, предлагаемый эксперимент направлен на использование сигналов вибрации редуктора для оценки серьезности поломок зубьев косозубых шестерен.Для этого один зуб косозубой шестерни Z1 был поврежден разной степени. С другой стороны, шестерня Z2 не претерпела изменений. Было учтено десять сценариев, то есть один для передачи Z1 в исправном состоянии, а остальные — для девяти уровней серьезности неисправности передачи Z1. Эти сценарии перечислены на рисунке 3 и в таблице 2.
| |||||||||||||||||||||||||||||||||||||||||
Мы также рассмотрели редуктор, работающий в различных условиях эксплуатации; то есть мы учли разные нагрузки и скорости вращения. Скорость вращения имела пять сценариев, в трех из которых она была постоянной, а в остальных — переменной. С другой стороны, нагрузка, прикладываемая магнитной тормозной системой, имела три сценария, в которых нагрузка имела постоянные значения.Эти сценарии подробно описаны в таблицах 3 и 4 для скоростей вращения и нагрузок соответственно.
| |||||||||||||||||||||||||||
| ||||||||||||||
Мы регистрировали каждую выборку вибросигнала за интервал времени 10 с. Кроме того, мы выполнили каждый комбинированный сценарий по три раза. Таким образом, база данных изначально состоит из 45 сигналов для каждой степени серьезности сбоя, то есть сбалансированная база данных из 450 сигналов, учитывающих все десять уровней серьезности. Величина этих сигналов была нормализована до диапазона [0, 1] и разделена на фрагменты длиной 0,25 секунды, в результате чего было получено 1800 сигналов для каждого уровня серьезности неисправности и 18000 сигналов во всей сбалансированной базе данных.
Кроме того, мы выполнили каждый комбинированный сценарий по три раза. Таким образом, база данных изначально состоит из 45 сигналов для каждой степени серьезности сбоя, то есть сбалансированная база данных из 450 сигналов, учитывающих все десять уровней серьезности. Величина этих сигналов была нормализована до диапазона [0, 1] и разделена на фрагменты длиной 0,25 секунды, в результате чего было получено 1800 сигналов для каждого уровня серьезности неисправности и 18000 сигналов во всей сбалансированной базе данных.
3.2. Экспериментальная установка: обучение системе классификации
Система, предложенная для оценки серьезности неисправности редуктора, основана на архитектуре глубокой сверточной нейронной сети.Таким образом, было необходимо двумерное представление входных сигналов. Мы решили представить их в частотно-временной области, так как такое представление позволяет визуализировать, когда возникают определенные частотные компоненты, связанные с отказом.
Кратковременное преобразование Фурье — это метод, который мы использовали для создания двумерного представления сигналов, то есть спектрограмм преобразования Фурье. STFT имеет низкие вычислительные затраты, чем другие методы частотно-временного представления [26].Эта характеристика особенно важна для предлагаемой системы, поскольку мы имеем дело с приложением реального времени. Конфигурация STFT включала окно Хэмминга размером 128 с перекрытием, равным 50%. Эти варианты сочетали селективное свойство окна Хэмминга с балансом между плавным изменением результирующего сигнала и низкими вычислительными затратами.
STFT имеет низкие вычислительные затраты, чем другие методы частотно-временного представления [26].Эта характеристика особенно важна для предлагаемой системы, поскольку мы имеем дело с приложением реального времени. Конфигурация STFT включала окно Хэмминга размером 128 с перекрытием, равным 50%. Эти варианты сочетали селективное свойство окна Хэмминга с балансом между плавным изменением результирующего сигнала и низкими вычислительными затратами.
Были разработаны два экспериментальных сценария. В первом из них информация о сигнале была сжата в изображения RGB размером 175 × 175 пикселей.Этот вид данных позволяет предоставить больше информации в систему оценки серьезности неисправности, поскольку могут использоваться такие уловки, как цветовые карты. С другой стороны, это увеличивает вычислительную нагрузку на систему, потому что вход представляет 3 канала. Во втором сценарии мы использовали изображения в оттенках серого 175 × 175 пикселей. В отличие от предыдущего сценария, единственная информация, предоставляемая спектрограммами, — это величина преобразования Фурье. На рисунке 4 показан пример спектрограммы, полученной описанным способом.
На рисунке 4 показан пример спектрограммы, полученной описанным способом.
Система классификации, используемая в этой работе, состоит из трех сверточных слоев, трех слоев максимального объединения, одного полностью связного слоя и одного выходного уровня. Поскольку выходы такой структуры представляют собой значения вероятности в диапазоне от 0 до 1, функция активации softmax использовалась в нейронах выходного слоя, а функция активации ReLU использовалась в нейронах остальных слоев. Согласно Монтейро и соавт., Эта архитектура обеспечивает удовлетворительные характеристики при оценке серьезности неисправностей редукторов.[10]. Это проиллюстрировано на рисунке 5. Кроме того, машина опорных векторов использовалась для анализа выходных данных системы и повышения ее производительности. Этот алгоритм уже использовался в подобных приложениях, например, предложенный Ли и др. [27], в котором SVM использовался для объединения результатов классификаторов, работающих с мультимодальными данными.
Что касается шага обучения, данные были разделены на три группы: обучение, тестирование и проверка. Мы использовали набор данных проверки, чтобы уменьшить возникновение проблем, связанных с переобучением.Каждый из них содержит соответственно 50%, 25% и 25% сбалансированных сигналов для каждого уровня серьезности неисправности. Тренировочный процесс проводился по 10-ти и 50-ти эпохным сценариям. Конфигурация компьютера, используемого для обучения модели, включала ОС Windows 10 Home, 64 бита, память (ОЗУ) 15,9 ГБ, процессор Intel® Core ™ i7-6500 CPU @ 2,50 ГГц × 2 и AMD Radeon ™ T5 M330 (без CUDA поддерживать).
4. Результаты и обсуждение
Первое обсуждение касается времени обучения системы диагностики неисправностей, основанной на глубоких сверточных нейронных сетях.Хорошо известно, что компьютеры с графическими процессорами намного лучше справляются с вычислительной нагрузкой, связанной с решениями глубокого обучения, чем компьютеры с процессорами. С другой стороны, компьютеры с графическими процессорами более дорогие, а это означает, что они не всегда доступны. Таблица 5 иллюстрирует эту проблему. Он показывает среднее время обучения 30 DCNN (в каждом сценарии) с архитектурой, упомянутой в последнем разделе, в отношении компьютеров с различными конфигурациями и набора данных изображения RGB. Модели обучались в 50 эпох.Мы обучили это количество моделей, чтобы гарантировать статистическую релевантность результатов. Первую компьютерную конфигурацию (компьютер с графическим процессором) использовали Монтейро и др. [10]. Он состоял из ОС Ubuntu 16.04 LTS, 64 бита, памяти 15,6 ГБ, процессора Intel Xeon (R) CPU E 5-2609 v3 @ 1,90 ГГц × 12 и графики Gallium 0.4 на NV117. Второй был представлен в предыдущем разделе.
С другой стороны, компьютеры с графическими процессорами более дорогие, а это означает, что они не всегда доступны. Таблица 5 иллюстрирует эту проблему. Он показывает среднее время обучения 30 DCNN (в каждом сценарии) с архитектурой, упомянутой в последнем разделе, в отношении компьютеров с различными конфигурациями и набора данных изображения RGB. Модели обучались в 50 эпох.Мы обучили это количество моделей, чтобы гарантировать статистическую релевантность результатов. Первую компьютерную конфигурацию (компьютер с графическим процессором) использовали Монтейро и др. [10]. Он состоял из ОС Ubuntu 16.04 LTS, 64 бита, памяти 15,6 ГБ, процессора Intel Xeon (R) CPU E 5-2609 v3 @ 1,90 ГГц × 12 и графики Gallium 0.4 на NV117. Второй был представлен в предыдущем разделе.
| ||||||||||||
Можно заметить, что процесс обучения для компьютера без GPU был намного дольше, чем для компьютера с GPU; я. е. было примерно в 13 раз дольше. В некоторых ситуациях, в зависимости от объема данных или доступного времени, использование компьютеров без графических процессоров может оказаться непрактичным.
е. было примерно в 13 раз дольше. В некоторых ситуациях, в зависимости от объема данных или доступного времени, использование компьютеров без графических процессоров может оказаться непрактичным.
Для решения этой проблемы можно сделать несколько вариантов. Уменьшение количества тренировочных эпох — одна из них. Как видно из Таблицы 6, уменьшение количества тренировочных эпох с 50 до 10 уменьшило среднее время тренировки примерно на 78,7%. С другой стороны, такое сокращение сказывается на производительности. Средняя точность снизилась примерно на 1.8%. Такое поведение уже ожидалось, поскольку у моделей было меньше итераций для изучения особенностей обучающих данных. Результаты в таблице 6 были получены путем обучения 30 сетей DCNN в каждом сценарии.
| ||||||||||||||||||
Прежде чем предлагать модификации системы диагностики неисправностей, необходимо определить основные трудности модели. В качестве эталона мы взяли модель, обученную за 10 эпох. В таблице 7 перечислены средние значения и значения стандартного отклонения точности для 30 моделей. Можно заметить, что для некоторых классов, например, P1 и P2, система показывала высокие значения точности, т.е. близкие к 100%.С другой стороны, модели показали низкую производительность для входных данных из таких классов, как P6 и P7.
| |||||||||||||||||||||||||||||||||||||||||
Этот анализ можно углубить, наблюдая за выходными данными классификатора.На рисунке 6 показано, как выходные вероятности моделей распределяются в соответствии с классом входного изображения. Что касается входов, принадлежащих к классу P1, можно заметить, что выходные вероятности моделей были очень близки к 1 для класса P1 и очень близки к 0 для других. Это помогает понять, почему точность модели для этого класса была 100%. С другой стороны, профили распределения, принадлежащие классам P6 и P7, показывают, что выходы сетей не были такими точными, как в предыдущем случае. Действительно, выбор только тех выходных данных, которые представляют наибольшее значение вероятности, может привести к неправильной классификации из-за значительного присутствия выбросов.
Действительно, выбор только тех выходных данных, которые представляют наибольшее значение вероятности, может привести к неправильной классификации из-за значительного присутствия выбросов.
Для решения этой проблемы мы предложили решение, основанное на использовании выходных вероятностей всех десяти классов для выполнения правильной классификации. Такое решение можно реализовать несколькими способами. Один из них — использование неглубоких классификаторов, например, многослойного персептрона или машины опорных векторов. Эти классификаторы идентифицируют класс серьезности передачи, используя информацию, содержащуюся в выходных вероятностях глубокой сверточной нейронной сети.Таким образом, отклик системы получается путем анализа распределения вероятностей, а не только одного значения.
В этом исследовании мы использовали машину опорных векторов. Он был обучен с выходными данными DCNN относительно ранее установленных данных обучения. Результаты предложенной модификации перечислены в таблицах 8 и 9.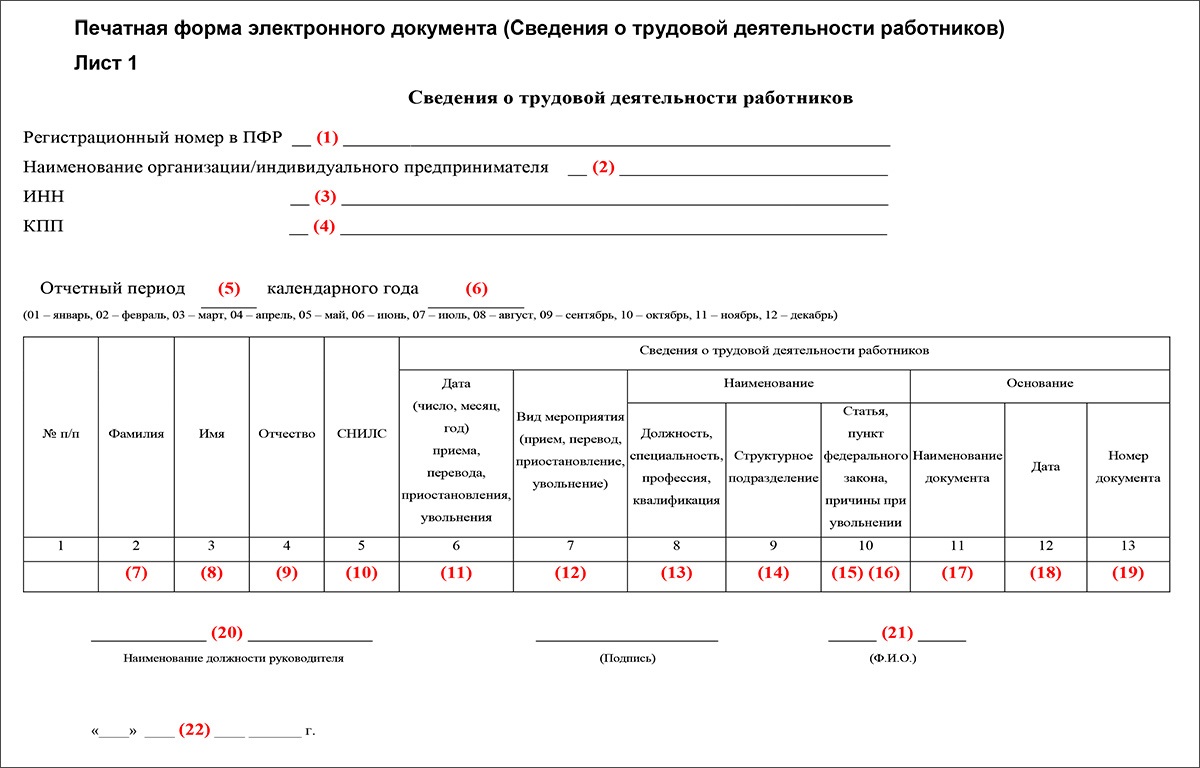 Таблица 8 показывает средние результаты каждого класса по 30 моделям и сравнивает их с результатами сценария без дополнительного классификатора. В таблице 9 показаны средние результаты для всех классов и моделей, а также в сравнении со сценарием без дополнительного классификатора.
Таблица 8 показывает средние результаты каждого класса по 30 моделям и сравнивает их с результатами сценария без дополнительного классификатора. В таблице 9 показаны средние результаты для всех классов и моделей, а также в сравнении со сценарием без дополнительного классификатора.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||
Из таблицы 8 можно сделать вывод, что включение классификатора улучшило характеристики модели по всем 10 классам , как в отношении средней точности, так и стандартного отклонения. Кроме того, из Таблицы 9 можно заметить, что средняя точность увеличилась примерно на 2,56% за счет увеличения менее чем на 1 секунду среднего времени обучения. Эти результаты еще более значительны по сравнению с результатами, полученными в процессе обучения с 50 эпохами, представленными в таблице 5. Средняя точность предложенной модели была только на 0,76% выше, но при среднем времени обучения на 78,64% меньше. Это значительно ускорило обучение системы диагностики неисправностей. Кроме того, мы использовали два дополнительных показателя, чтобы гарантировать надежность полученных результатов: F -score и AUC. Первый — это среднее гармоническое значение точности и отзыва.Второй показатель, с другой стороны, определяется как площадь под кривой рабочей характеристики приемника (ROC). Их средние значения перечислены в Таблице 10, и оба они показывают тенденцию к улучшению, совпадающую с тенденцией, наблюдаемой в Таблице 9, то есть система диагностики с классификатором представила значения для показателей примерно на 2% выше, чем без классификатора.
Эти результаты еще более значительны по сравнению с результатами, полученными в процессе обучения с 50 эпохами, представленными в таблице 5. Средняя точность предложенной модели была только на 0,76% выше, но при среднем времени обучения на 78,64% меньше. Это значительно ускорило обучение системы диагностики неисправностей. Кроме того, мы использовали два дополнительных показателя, чтобы гарантировать надежность полученных результатов: F -score и AUC. Первый — это среднее гармоническое значение точности и отзыва.Второй показатель, с другой стороны, определяется как площадь под кривой рабочей характеристики приемника (ROC). Их средние значения перечислены в Таблице 10, и оба они показывают тенденцию к улучшению, совпадающую с тенденцией, наблюдаемой в Таблице 9, то есть система диагностики с классификатором представила значения для показателей примерно на 2% выше, чем без классификатора.
| ||||||||||||||||||
Что касается среднего времени для выполнения классификации одного единственного входа, добавление стадии принятия решения не привело к существенные изменения. Действительно, среднее время классификации, составлявшее около 0,03 секунды без этапа принятия решения, увеличилось менее чем на 0,001 секунды.
Чтобы оценить, насколько значительными были улучшения, обеспечиваемые предложенным решением, ранжированный по сигналу статистический тест Вилкоксона может быть применен к выходам систем диагностики неисправностей с этапом принятия решения и без него.Результаты приведены в таблице 10. Тест Вилкоксона — это непараметрический тест гипотезы, который можно использовать для оценки того, эквивалентны ли два распределения или нет [28]. Если это не так, это означает, что произошло статистически значимое улучшение (символ Λ).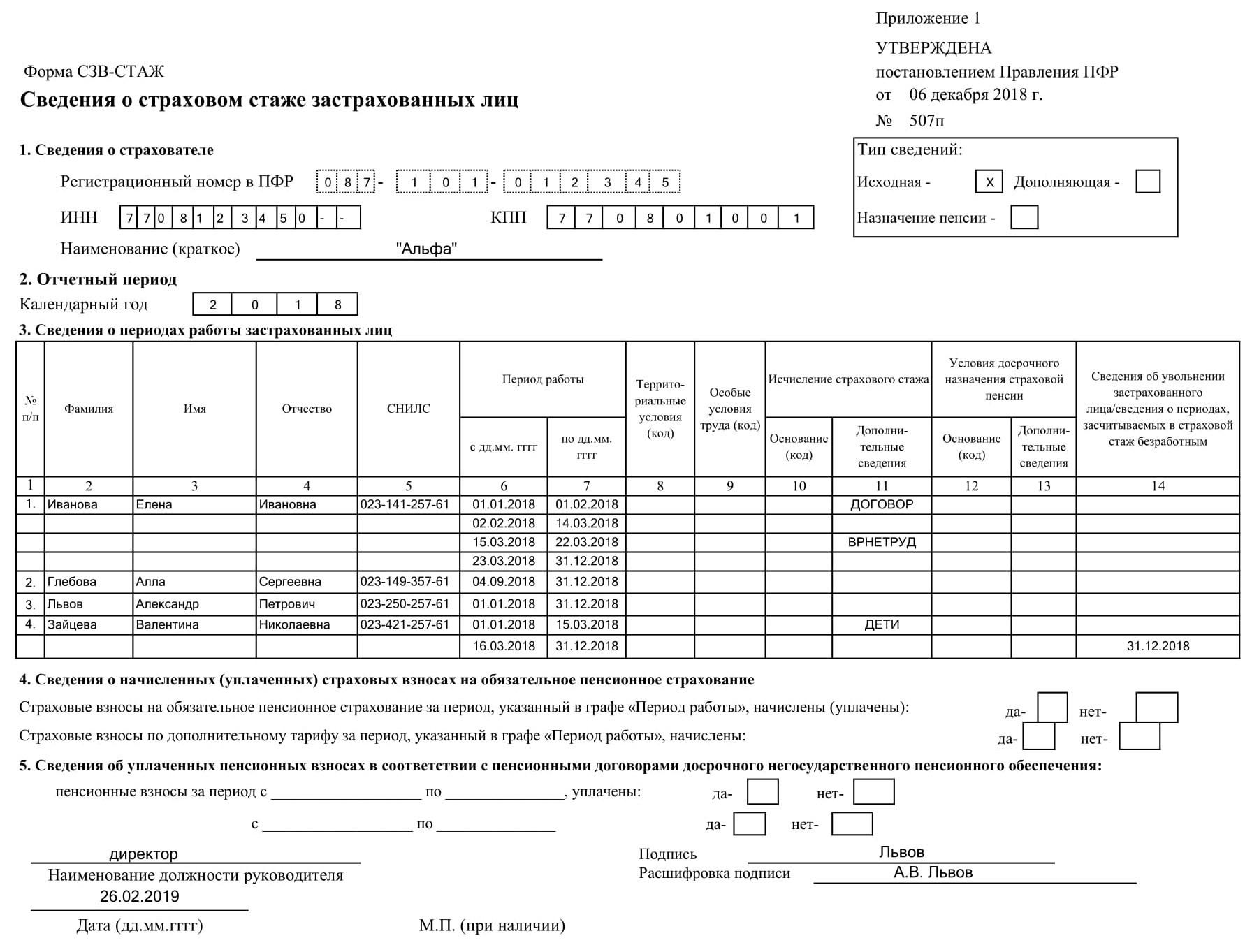 В противном случае улучшение не было значительным (- символ). Таблица 11 показывает, что у нас были значительные улучшения для классов P4, P5, P6, P7 и P9. Хотя остальные классы также показали некоторое улучшение, они не были статистически значимыми.
В противном случае улучшение не было значительным (- символ). Таблица 11 показывает, что у нас были значительные улучшения для классов P4, P5, P6, P7 и P9. Хотя остальные классы также показали некоторое улучшение, они не были статистически значимыми.
| |||||||||||||||||||||||||||||
Мы также проанализировали производительность этапа принятия решения, когда применялся другой алгоритм классификации. Этот алгоритм представлял собой многослойный персептрон, т.е. нейронную сеть. Мы устанавливаем размер входного слоя равным 10, скрытого слоя с 21 нейроном и выходного слоя с одним нейроном. Мы развернули логистическую сигмоиду в качестве функции активации. Мы установили количество эпох обучения равным 200. Количество обучающих, тестовых и проверочных выборок осталось таким же, как в сценарии SVM. Мы обучили 30 MLP, чтобы гарантировать статистическую релевантность результатов. Мы показываем результаты для SVM и MLP в таблицах 12 и 13.В таблице 12 перечислены средние значения F 1-балла, AUC и точности. В Таблице 13 указано среднее время тренировки и бега.
Этот алгоритм представлял собой многослойный персептрон, т.е. нейронную сеть. Мы устанавливаем размер входного слоя равным 10, скрытого слоя с 21 нейроном и выходного слоя с одним нейроном. Мы развернули логистическую сигмоиду в качестве функции активации. Мы установили количество эпох обучения равным 200. Количество обучающих, тестовых и проверочных выборок осталось таким же, как в сценарии SVM. Мы обучили 30 MLP, чтобы гарантировать статистическую релевантность результатов. Мы показываем результаты для SVM и MLP в таблицах 12 и 13.В таблице 12 перечислены средние значения F 1-балла, AUC и точности. В Таблице 13 указано среднее время тренировки и бега.
| ||||||||||||||||||||||||
| ||||||||||||||||||
Что касается показателей, несмотря на небольшое преимущество, представленное этапом принятия решения SVM в отношении точности, был предложен тест Уилкоксона. что результаты, достигнутые обоими алгоритмами, были одинаковыми.Это означает, что предлагаемое решение может быть реализовано с другими классификаторами, кроме SVM. С другой стороны, интересный факт возникает из времени тренировок и бега. Процесс обучения на этапе принятия решения MLP был примерно в 7,1 раза дольше, чем у SVM, тогда как время выполнения было более чем в 20 раз быстрее. Правильное решение с учетом этого компромисса может быть привлекательным в зависимости от предполагаемого приложения.
Правильное решение с учетом этого компромисса может быть привлекательным в зависимости от предполагаемого приложения.
Эти анализы с этапом принятия решения SVM были также выполнены в отношении изображений спектрограммы в градациях серого.Они стремились оценить, как система диагностики неисправностей справится с сокращением доступной информации. Таблица 14 показывает среднюю точность и среднее время обучения для 30 моделей, относящихся к каждому сценарию. В этих сценариях рассматривались модели, обученные с использованием изображений RGB и изображений в градациях серого для 10 эпох. При расчете средней точности использовались только тестовые данные. Один заметил, что модель, обученная с использованием изображений RGB, дает лучшие результаты в отношении точности, то есть примерно на 10% выше.С другой стороны, среднее время обучения моделей, обученных с изображениями в оттенках серого, было меньше. Вероятно, это произошло из-за меньшего количества обработанной информации.
| ||||||||||||||||||
Таблица 15 и рисунок 7 помогают понять, что происходит с производительностью модели классификации, обученной с использованием изображений в градациях серого, относительно всех десяти классов. Можно заметить, что относительно сценария RGB даже результаты классов, подобных P1, ухудшились как по средней точности, так и по стандартному отклонению. На рисунке 7 показано, как вероятности выхода DCNN распределяются в соответствии с классом входного изображения.Для другого сценария количество выбросов значительно увеличилось. Такое поведение произошло со всеми классами.
| |||||||||||||||||||||||||||||||||||||||||
Также в этом сценарии используется новый сценарий , мы намерены оценить, может ли предлагаемое решение улучшить производительность классификатора на основе DCNN, используя выходные вероятности всех 10 классов.
Результаты, полученные с использованием машины опорных векторов, обученной с выходными данными глубоких сверточных нейронных сетей, перечислены в таблицах 16 и 17. Таблица 16 показывает средние результаты для каждого класса относительно 30 обученных моделей. Эти результаты сравниваются с результатами сценария без дополнительного классификатора.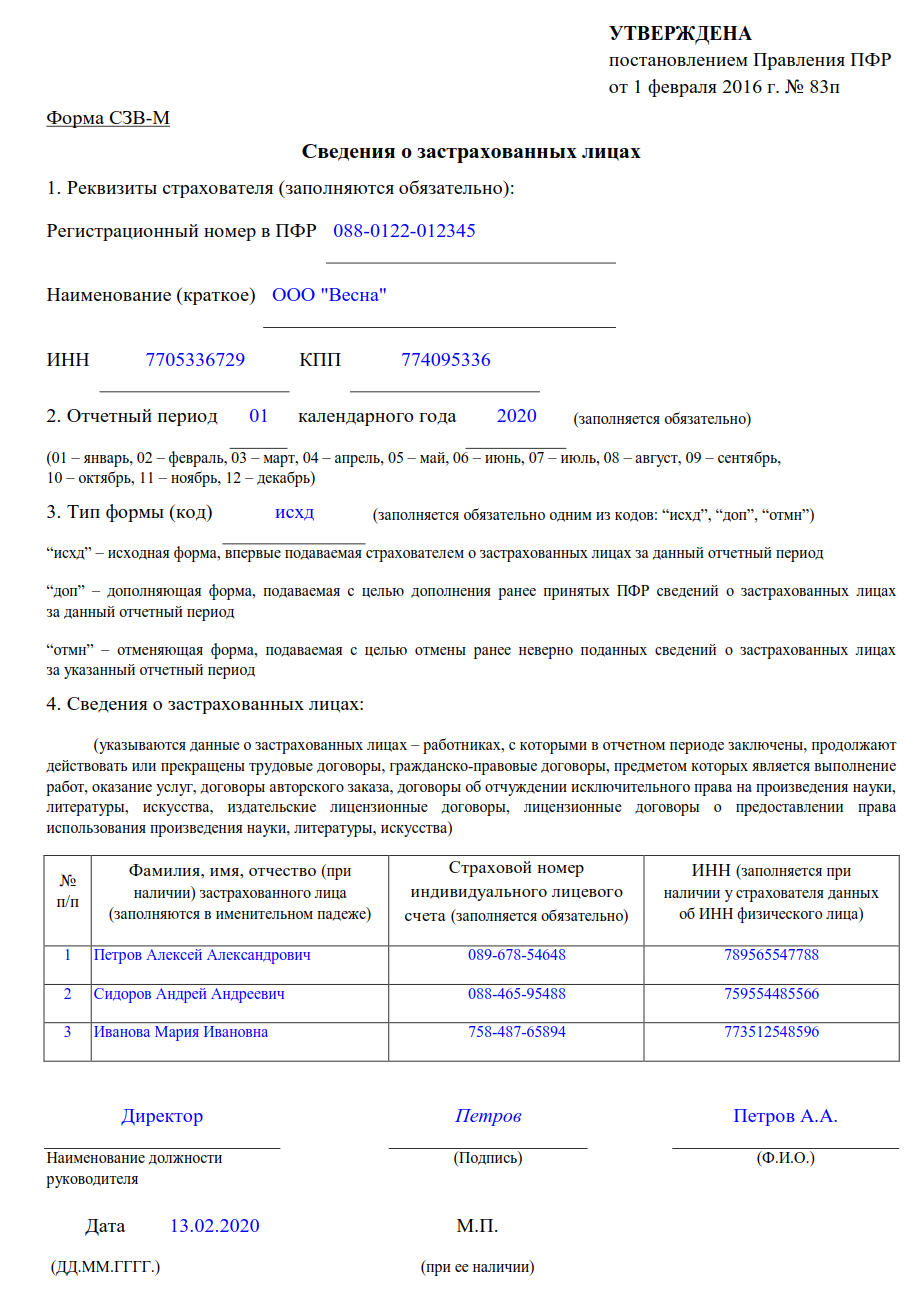 Таблица 17 показывает средние результаты по всем классам и моделям, а также сравнивает их со сценарием без дополнительной стадии. Из таблицы 16 можно сделать вывод, что включение классификатора улучшило производительность модели по всем десяти классам, как в отношении средней точности, так и стандартного отклонения.С другой стороны, даже эти улучшенные системы не смогли превзойти те, которые обучены с изображениями спектрограмм RGB, как видно из таблицы 14. Кроме того, из таблицы 17 можно заметить, что средняя точность увеличилась примерно на 4,18% за счет уменьшения менее 1 секунды до среднего времени обучения. Это относительное улучшение было выше, чем в предыдущем экспериментальном сценарии. В таблице 18 показаны средние значения F и AUC для систем с этапом принятия решения и без него.В таблице 18 показаны средние значения F и AUC для систем с этапом принятия решения и без него. Эти два показателя усиливают тенденцию к улучшению, вызванную добавлением стадии принятия решения.
Таблица 17 показывает средние результаты по всем классам и моделям, а также сравнивает их со сценарием без дополнительной стадии. Из таблицы 16 можно сделать вывод, что включение классификатора улучшило производительность модели по всем десяти классам, как в отношении средней точности, так и стандартного отклонения.С другой стороны, даже эти улучшенные системы не смогли превзойти те, которые обучены с изображениями спектрограмм RGB, как видно из таблицы 14. Кроме того, из таблицы 17 можно заметить, что средняя точность увеличилась примерно на 4,18% за счет уменьшения менее 1 секунды до среднего времени обучения. Это относительное улучшение было выше, чем в предыдущем экспериментальном сценарии. В таблице 18 показаны средние значения F и AUC для систем с этапом принятия решения и без него.В таблице 18 показаны средние значения F и AUC для систем с этапом принятия решения и без него. Эти два показателя усиливают тенденцию к улучшению, вызванную добавлением стадии принятия решения.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Средняя точность (%) | Среднее время обучения (с) | |
| Без классификатора | 84. 98 98 | 1967 |
| С классификатором | 89,16 | 1968 |
| |||||||||||||||||
Что касается среднего времени классификации, в этом сценарии добавление стадии принятия решения также не привело к значительным изменениям. Оно увеличилось с 0,022 секунды до менее 0,023 секунды.
Чтобы оценить, насколько значительным было улучшение, обеспечиваемое предложенным решением в этом новом сценарии, статистический тест Уилкоксона с ранжированием сигналов также был применен к выходам систем диагностики неисправностей с этапом принятия решения и без него. Результаты перечислены в таблице 19, которая показывает, что мы добились значительных улучшений для классов P4, P5, P6, P7, P8 и P10. Еще раз, хотя другие классы также показали улучшения, они не были значительными.
Результаты перечислены в таблице 19, которая показывает, что мы добились значительных улучшений для классов P4, P5, P6, P7, P8 и P10. Еще раз, хотя другие классы также показали улучшения, они не были значительными.
| ||||||||||||||||||||||||||||
5.Выводы
Мы проанализировали использование этапа принятия решения для интерпретации выходных данных системы диагностики неисправностей, основанной на глубоких сверточных нейронных сетях.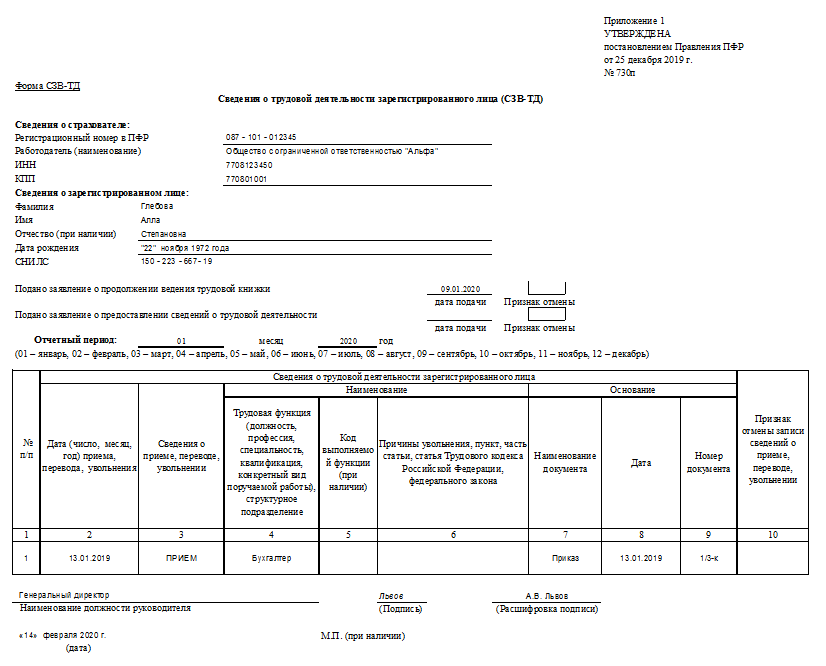 Эти выходы соответствуют вероятности того, что вход принадлежит классам данного набора. Таким образом, вместо использования традиционного подхода, такого как выбор класса с наибольшим значением вероятности, мы проанализировали выходное распределение глубокого классификатора, чтобы выполнить более надежную диагностику неисправностей.
Эти выходы соответствуют вероятности того, что вход принадлежит классам данного набора. Таким образом, вместо использования традиционного подхода, такого как выбор класса с наибольшим значением вероятности, мы проанализировали выходное распределение глубокого классификатора, чтобы выполнить более надежную диагностику неисправностей.
Результаты показали, что мы можем повысить точность системы классификации и сократить почти 80% времени обучения без ущерба для времени выполнения, которое увеличилось примерно на 0.001 секунда. Это улучшение особенно важно для ситуаций, в которых мощное оборудование, например графические процессоры, недоступно. Таким образом, система диагностики неисправностей с заданным значением точности может быть получена с использованием лишь небольшой части времени обучения, которое потребовалось бы для выполнения полного обучения. Эти результаты были достигнуты за счет использования SVM в качестве принимающего решения, который имел выходные вероятности исходной системы диагностики неисправностей в качестве входной информации. Аналогичные результаты были достигнуты при внедрении MLP в качестве лица, принимающего решения. Это предполагает, что предлагаемое решение также может быть реализовано с помощью алгоритмов, отличных от SVM.
Аналогичные результаты были достигнуты при внедрении MLP в качестве лица, принимающего решения. Это предполагает, что предлагаемое решение также может быть реализовано с помощью алгоритмов, отличных от SVM.
Мы также оценили использование входных спектрограмм RGB и оттенков серого. Хотя добавление стадии принятия решения привело к улучшениям в обоих сценариях, эти улучшения имели разные масштабы. Точность систем, работающих с изображениями в градациях серого, повысилась больше, чем в другом сценарии. Однако конечная точность этих систем, обученных на изображениях RGB, была лучше.Такое поведение можно объяснить количеством информации, доступной в каждом виде изображения, как обсуждалось ранее. Кроме того, мы увидели, что разница во времени выполнения в обоих сценариях не была существенной в отношении абсолютных значений. Таким образом, это предполагает, что использование изображений RGB не поставит под угрозу работу системы в приложениях реального времени.
Будущие работы касаются применения этой методологии диагностики неисправностей к другим видам отказов и для проблем, относящихся к различным физическим областям, например. g., диагностика неисправностей с помощью акустики. Более того, мы можем оценить производительность других алгоритмов, используемых в качестве лиц, принимающих решения.
g., диагностика неисправностей с помощью акустики. Более того, мы можем оценить производительность других алгоритмов, используемых в качестве лиц, принимающих решения.
Доступность данных
Данные, использованные для подтверждения результатов этого исследования, включены в статью.
Конфликт интересов
Авторы заявляют, что у них нет конфликта интересов.
Полное руководство по опорных векторов (SVM) | Марко Пейшейро
Поймите его внутреннюю работу и реализуйте SVM в четырех различных сценариях
Что бы мы делали без sklearn?Мы увидели, как подойти к проблеме классификации с помощью логистической регрессии, LDA и деревьев решений.Теперь появился еще один инструмент для классификации: машина опорных векторов .
Машина опорных векторов является обобщением классификатора под названием классификатор максимальной маржи . Классификатор максимальной маржи прост, но его нельзя применить к большинству наборов данных, поскольку классы должны быть разделены линейной границей.
Вот почему классификатор опорных векторов был введен как расширение классификатора максимальной маржи, которое может применяться в более широком диапазоне случаев.
Наконец, машина опорных векторов — это просто дальнейшее расширение классификатора опорных векторов для учета нелинейных границ классов.
Может использоваться как для двоичной, так и для мультиклассовой классификации.
Изложение теории SVM может быть очень техническим. Надеюсь, эта статья упростит понимание того, как работают SVM.
Когда теория раскрыта, вы сможете реализовать алгоритм в четырех различных сценариях!
Без дополнительной оплаты, перейдем к делу.
Нет SVM-гифок .. поэтому мне пришлось довольствоваться «машинным» gifЧтобы найти практические видеоуроки по машинному обучению, глубокому обучению и искусственному интеллекту, посетите мой канал YouTube.
Этот метод основан на разделении классов с помощью гиперплоскости.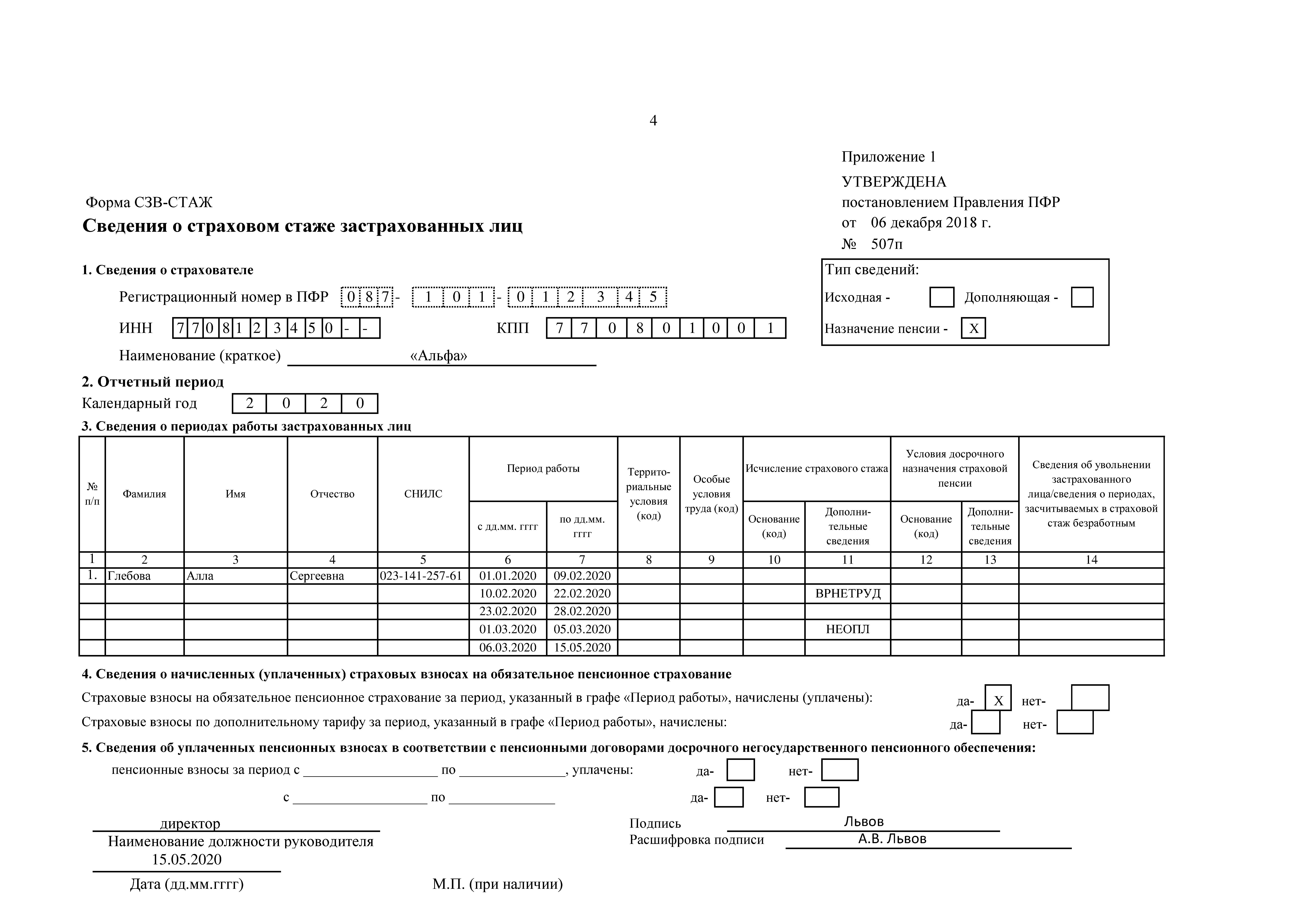
Что такое гиперплоскость?
В пространстве размерности p гиперплоскость — это плоское аффинное подпространство размерности p-1 . Визуально в 2D-пространстве гиперплоскость будет линией, а в 3D-пространстве — плоской.
Математически гиперплоскость выглядит просто:
Общее уравнение гиперплоскостиЕсли X удовлетворяет приведенному выше уравнению, то точка лежит на плоскости. В противном случае он должен быть на одной стороне плоскости, как показано ниже.
Линия представляет собой гиперплоскость в двухмерном пространстве. Точки, удовлетворяющие приведенному выше уравнению, будут лежать на линии, а другие — по одну сторону от плоскости.В общем, если данные могут быть идеально разделены с помощью гиперплоскости, то существует бесконечное количество гиперплоскостей, поскольку их можно сдвинуть вверх или вниз или немного повернуть, не соприкасаясь с наблюдением.
Вот почему мы используем гиперплоскость максимального запаса или оптимальную разделяющую гиперплоскость , которая является самой удаленной от наблюдений разделяющей гиперплоскостью. Мы вычисляем перпендикулярное расстояние от каждого тренировочного наблюдения с учетом гиперплоскости. Это поле известно как маржа . Следовательно, оптимальная разделяющая гиперплоскость — это гиперплоскость с наибольшим запасом.
Мы вычисляем перпендикулярное расстояние от каждого тренировочного наблюдения с учетом гиперплоскости. Это поле известно как маржа . Следовательно, оптимальная разделяющая гиперплоскость — это гиперплоскость с наибольшим запасом.
Как вы можете видеть выше, есть три точки, равноудаленные от гиперплоскости.Эти наблюдения известны как опорных векторов , потому что, если их положение смещается, гиперплоскость также смещается. Интересно, что это означает, что гиперплоскость зависит только от опорных векторов, а не от каких-либо других наблюдений.
Что делать, если разделяющей плоскости не существует?
Перекрывающиеся классы, в которых не существует разделяющей гиперплоскости. В этом случае классификатор максимального поля отсутствует. Мы используем классификатор опорных векторов, который может почти разделить классы с помощью мягкого поля , называемого классификатором опорных векторов . Однако дальнейшее обсуждение этого метода становится очень техническим, и, поскольку это не самый идеальный подход, мы пока пропустим эту тему.
Однако дальнейшее обсуждение этого метода становится очень техническим, и, поскольку это не самый идеальный подход, мы пока пропустим эту тему.
Машина опорных векторов — это расширение классификатора опорных векторов, которое является результатом увеличения пространства признаков с использованием ядер . Подход ядра — это просто эффективный вычислительный подход для размещения нелинейной границы между классами.
Не вдаваясь в технические подробности, ядро - это функция, которая количественно определяет сходство двух наблюдений.Ядро может быть любой степени. Использование ядра со степенью больше единицы приводит к более гибкой границе принятия решений, как показано ниже.
Пример классификации с SVMЧтобы лучше понять, как выбор ядра может повлиять на алгоритм SVM, давайте реализуем его в четырех различных сценариях.
Этот проект разделен на четыре мини-проекта.
В первой части будет показано, как выполнить классификацию с линейным ядром и как параметр регуляризации C влияет на результирующую гиперплоскость .
Затем во второй части будет показано, как работать с гауссовским ядром для создания нелинейной гиперплоскости.
Третья часть моделирует перекрывающиеся классы, и мы будем использовать перекрестную проверку , чтобы найти лучшие параметры для SVM.
Наконец, мы выполняем очень простой классификатор спама , используя SVM.
Упражнения, указанные выше, были взяты из курса Эндрю Нга, доступного бесплатно на Coursera. Я просто решаю их с помощью Python, что не рекомендуется инструктором.Тем не менее, я очень рекомендую курс всем новичкам.
Как всегда, записная книжка и данные доступны здесь.
Мини-проект 1 — SVM с линейным ядром
Прежде чем мы начнем, давайте импортируем несколько полезных библиотек:
Обратите внимание, что мы импортируем loadmat здесь, потому что наши данные находятся в матричной форме.
Затем мы сохраняем пути к нашим наборам данных в различных переменных:
Наконец, мы создадим функцию, которая поможет нам быстро построить каждый набор данных:
Отлично!
Теперь, в этой части, мы реализуем машину опорных векторов с использованием линейного ядра и увидим, как параметр регуляризации может повлиять на гиперплоскость.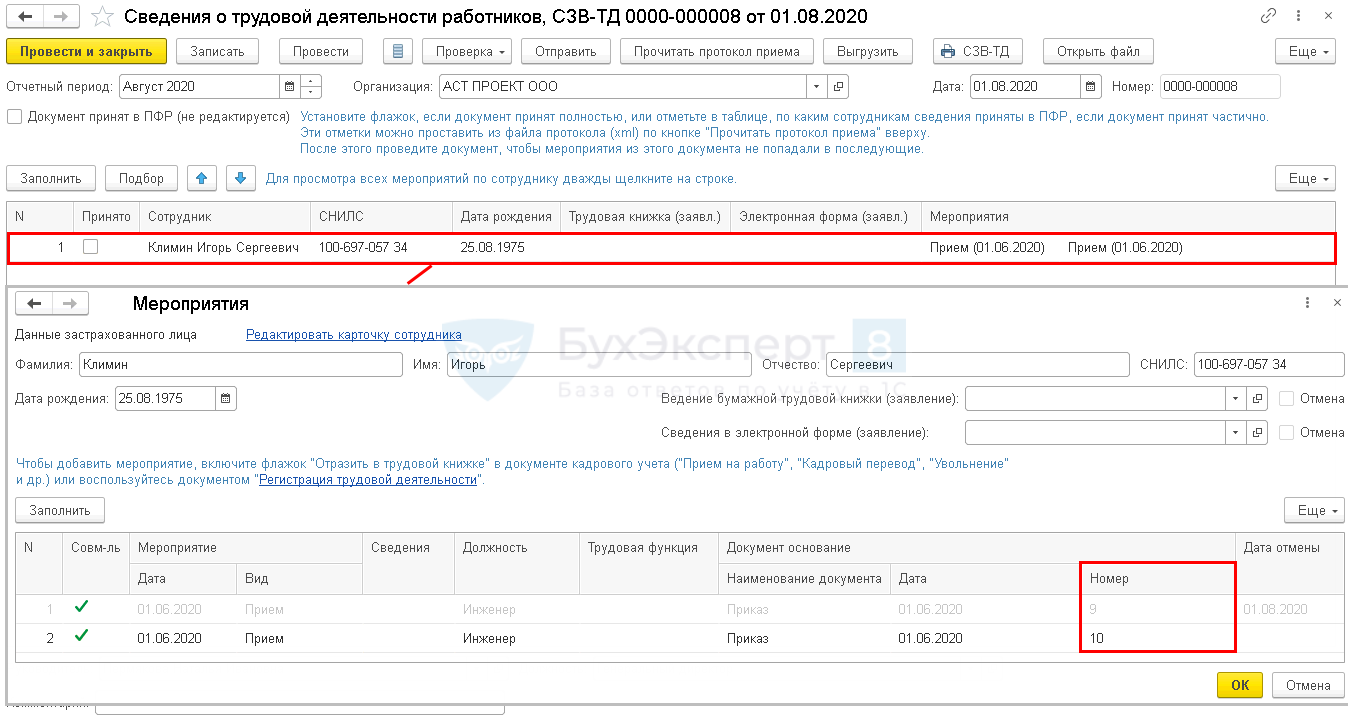
Во-первых, загрузим и визуализируем данные:
И вы должны увидеть:
Обратите внимание на графике выше на наличие выброса с левой стороны . Давайте посмотрим, как параметр регуляризации повлияет на гиперплоскость при наличии выброса.
Приведенный выше блок кода просто подгоняет SVM к данным, и мы используем прогнозы для построения гиперплоскости. Обратите внимание, что мы используем параметр регуляризации, равный 1. Результат должен быть следующим:
Гиперплоскость с C = 1Как вы можете видеть, гиперплоскость проигнорировала выброс.Следовательно, низкий параметр регуляризации будет , лучше обобщить . Ошибка теста обычно выше, чем ошибка перекрестной проверки.
Теперь давайте увеличим параметр регуляризации:
И вы получите:
Гиперплоскость с C = 100 Теперь выброс находится на правой стороне гиперплоскости, но это также означает, что мы переоснащаем. В конечном итоге эта граница не будет работать с ненаблюдаемыми данными.
Мини-проект 2 — SVM с гауссовым ядром
Теперь мы знаем, что для учета нелинейных границ нам нужно изменить функцию ядра.В этом упражнении мы будем использовать гауссово ядро .
Сначала построим график наших данных:
И вы должны увидеть:
Перед реализацией SVM вы должны знать, что ядро Гаусса выражается как:
Функция ядра ГауссаОбратите внимание, что существует параметр сигма , который определяет как быстро показатель сходства стремится к нулю, когда они находятся дальше друг от друга.
Следовательно, реализуем это следующим кодом:
И у вас должна получиться следующая гиперплоскость:
Нелинейная гиперплоскость с гауссовым ядромУдивительно! Гиперплоскость не идеальная граница, но она неплохо справилась с классификацией большей части данных.Я предлагаю вам попробовать различные значения сигма , чтобы увидеть, как это влияет на гиперплоскость.
Мини-проект 3 — SVM с перекрестной проверкой
Перекрестная проверка необходима для выбора наилучших параметров настройки для оптимальной производительности нашей модели. Давайте посмотрим, как это можно применить к SVM.
Давайте посмотрим, как это можно применить к SVM.
Конечно, давайте посмотрим, как выглядят данные для этого упражнения:
И вы получите:
Обратите внимание, что у нас есть перекрывающиеся классы. Конечно, наша гиперплоскость не будет идеальной, но мы будем использовать перекрестную проверку, чтобы убедиться, что это лучшее, что мы можем получить:
Из приведенной выше ячейки кода вы должны получить, что лучший параметр регуляризации равен 1, и что сигма должна быть 0.1. Используя эти значения, мы можем сгенерировать гиперплоскость:
И получить:
Гиперплоскость с C = 1 и sigma = 0,1Мини-проект 4 — Классификация спама с помощью SVM
Наконец, мы обучаем классификатор спама с помощью SVM. В этом случае мы будем использовать линейное ядро. Кроме того, у нас есть отдельные наборы данных для обучения и тестирования, что немного упростит наш анализ.
И вы видите, что мы получаем точность обучения 99,825% и точность теста 98,9%!
SVM: выбор функций и ядра | автор: Пьер Паоло Ипполито
Точки данных на одной стороне гиперплоскости будут классифицированы в определенный класс, в то время как точки данных на другой стороне гиперплоскости будут классифицированы в другой класс (например,зеленый и красный, как на рисунке 2). Расстояние между гиперплоскостью и первой точкой (для всех различных классов) по обе стороны от гиперплоскости является мерой уверенности в том, что алгоритм принимает решение о классификации. Чем больше расстояние и тем увереннее мы можем быть, SVM принимает правильное решение.
Расстояние между гиперплоскостью и первой точкой (для всех различных классов) по обе стороны от гиперплоскости является мерой уверенности в том, что алгоритм принимает решение о классификации. Чем больше расстояние и тем увереннее мы можем быть, SVM принимает правильное решение.
Точки данных, ближайшие к гиперплоскости, называются опорными векторами. Опорные векторы определяют ориентацию и положение гиперплоскости, чтобы максимизировать поле классификатора (и, следовательно, оценку классификации).Количество опорных векторов, которые должен использовать алгоритм SVM, может быть произвольно выбрано в зависимости от приложений.
Базовая классификация SVM может быть легко реализована с помощью библиотеки Scikit-Learn Python в несколько строк кода.
из sklearn import svm
trainingsvm = svm.SVC (). Fit (X_Train, Y_Train)
predictionsvm = trainingsvm.predict (X_Test)
print (confusion_matrix (Y_Test, predictionsvm))
print (classification_report) (Y_vm_report)
Существует два основных типа алгоритмов классификации SVM Hard Margin и Soft Margin:
- Hard Margin: направлен на поиск наилучшей гиперплоскости, не допуская никаких форм ошибочной классификации.

- Мягкое поле: мы добавляем степень допуска в SVM. Таким образом, мы позволяем модели добровольно ошибочно классифицировать несколько точек данных, если это может привести к идентификации гиперплоскости, способной лучше обобщать невидимые данные.
Soft Margin SVM может быть реализован в Scikit-Learn путем добавления штрафного члена C в svm.SVC . Чем больше C, тем больше штраф получает алгоритм при ошибочной классификации.
Если данные, с которыми мы работаем, не разделимы линейно (что приводит к плохим результатам линейной классификации SVM), можно применить метод, известный как трюк с ядром.Этот метод может отображать наши нелинейные разделяемые данные в пространство более высокой размерности, делая наши данные линейно разделяемыми. Используя это новое размерное пространство, можно легко реализовать SVM (рис. 3).
Рисунок 3: Уловка с ядром [3] Существует много различных типов ядер, которые можно использовать для создания этого пространства более высокой размерности, некоторые примеры — линейные, полиномиальные, сигмоидальные и радиальные базисные функции (RBF). В Scikit-Learn функция ядра может быть указана путем добавления параметра ядра в
В Scikit-Learn функция ядра может быть указана путем добавления параметра ядра в svm.SVC . Можно включить дополнительный параметр под названием гамма, чтобы указать влияние ядра на модель.
Обычно предлагается использовать линейные ядра, если количество объектов больше, чем количество наблюдений в наборе данных (иначе RBF может быть лучшим выбором).
При работе с большим объемом данных с использованием RBF скорость может стать ограничением, которое необходимо учитывать.
После установки нашей линейной SVM можно получить доступ к коэффициентам классификатора, используя .coef_ на обученной модели. Эти веса определяют координаты ортогональных векторов, ортогональных гиперплоскости. Их направление представляет вместо этого предсказанный класс.
Следовательно, важность характеристики может быть определена путем сравнения размеров этих коэффициентов друг с другом. Таким образом, глядя на коэффициенты SVM, можно определить основные характеристики, используемые при классификации, и избавиться от неважных (которые имеют меньшую дисперсию).
Уменьшение количества функций в машинном обучении играет действительно важную роль, особенно при работе с большими наборами данных.Фактически это может: ускорить обучение, избежать переобучения и, в конечном итоге, привести к лучшим результатам классификации благодаря уменьшению шума в данных.
На рисунке 4 показаны основные особенности, которые я определил с помощью SVM в базе данных диабета индейцев пима. Зеленым цветом показаны все характеристики, соответствующие отрицательным коэффициентам, а синим — положительным. Если вы хотите узнать об этом больше, весь мой код находится в свободном доступе в моих профилях Kaggle и GitHub.
Машина опорных векторов на Python.Эта статья представляет собой исчерпывающее руководство… | by Wajiha Urooj | Edureka
Машинное обучение — это революция нового века в компьютерную эру. Мы можем выполнять задачи, о которых можно только мечтать, с правильным набором данных и соответствующими алгоритмами для обработки данных для получения оптимальных результатов. В этой статье мы рассмотрим один из таких алгоритмов классификации в машинном обучении с использованием python, то есть Support Vector Machine в Python. В этом блоге рассматриваются следующие темы:
В этой статье мы рассмотрим один из таких алгоритмов классификации в машинном обучении с использованием python, то есть Support Vector Machine в Python. В этом блоге рассматриваются следующие темы:
- Введение в машинное обучение
- Что такое машина опорных векторов
- Как работает SVM?
- Ядра SVM
- Сценарии использования машины опорных векторов
- Пример SVM
Машинное обучение — это процесс подачи в машину достаточного количества данных для обучения и прогнозирования возможного результата с использованием алгоритмов.Чем больше данных поступает в машину, тем эффективнее становится машина. Попробуем разобраться в этом на примере из жизни.
Я уверен, что большинству из вас известны прогнозы, сделанные в любом виде спорта перед любым крупным матчем. В данном случае возьмем пример футбольной пенальти.
Учитываются данные предыдущих игр, допустим, вратарь сохранил все пенальти справа от себя в последних 50 отобранных им пенальти.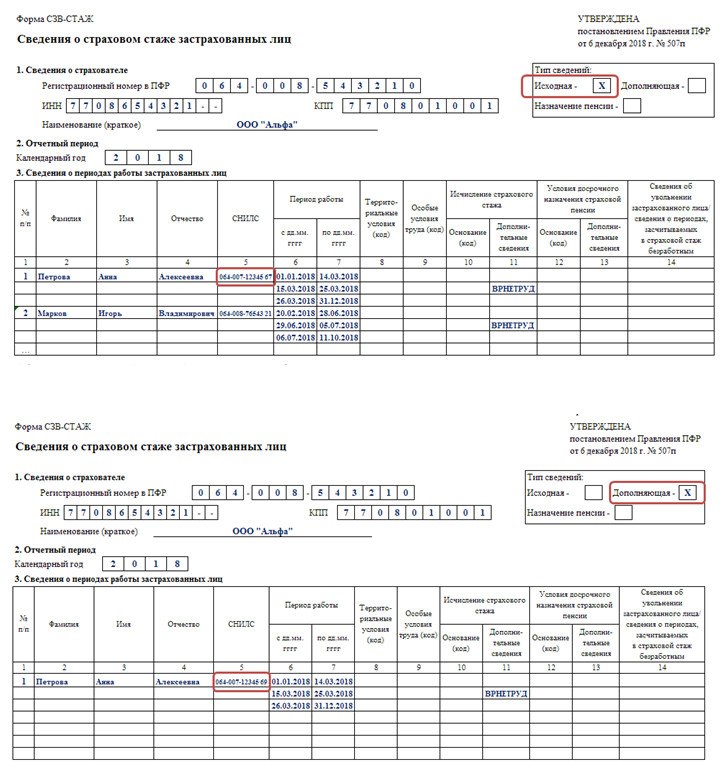 Эти данные будут иметь решающее значение для прогнозирования того, спасет ли он следующие штрафные санкции или нет.Есть и другие факторы, которые следует учитывать.
Эти данные будут иметь решающее значение для прогнозирования того, спасет ли он следующие штрафные санкции или нет.Есть и другие факторы, которые следует учитывать.
Другой пример — предложения, которые мы получаем во время серфинга в Интернете, данные наших предыдущих выборов обрабатываются, чтобы предоставить нам наиболее благоприятный контент, который мы, скорее всего, будем смотреть.
В любом случае, машинное обучение — это не просто загрузка в машину большого количества данных, для получения оптимальных результатов требуется множество процессов, алгоритмов и решающих факторов.
В этом блоге мы рассмотрим один из таких алгоритмов векторной поддержки, чтобы понять, как он работает с python.Перед этим давайте также рассмотрим типы машинного обучения.
- Контролируемое обучение — Обучение осуществляется контролируемым образом, чтобы соответствующим образом контролировать результат. Это, как следует из названия, контролируется таким образом, чтобы машина узнала то, что пользователь хочет, чтобы она узнала.

- Неконтролируемое обучение — В этом случае машина просто исследует предоставленные ей данные. Иногда данные без меток и категорий, и машина делает возможные ссылки и прогнозы без какого-либо надзора.
- Обучение с подкреплением — По сути, это означает принудительное применение модели поведения. Машине необходимо установить систематический подход к обучению с подкреплением.
Машина опорных векторов была впервые представлена в 1960-х, а затем импровизирована в 1990-х. Это алгоритм классификации машинного обучения с учителем, который стал чрезвычайно популярным в настоящее время благодаря своим чрезвычайно эффективным результатам.
SVM реализована несколько иначе, чем другие алгоритмы машинного обучения.Он способен выполнять классификацию, регрессию и обнаружение выбросов.
Машина опорных векторов — это дискриминантный классификатор, который формально разработан разделительной гиперплоскостью. Это представление примеров в виде точек в пространстве, которые нанесены на карту так, чтобы точки разных категорий были разделены как можно более широким промежутком. В дополнение к этому SVM также может выполнять нелинейную классификацию. Давайте посмотрим, как работает машина опорных векторов.
Это представление примеров в виде точек в пространстве, которые нанесены на карту так, чтобы точки разных категорий были разделены как можно более широким промежутком. В дополнение к этому SVM также может выполнять нелинейную классификацию. Давайте посмотрим, как работает машина опорных векторов.
- Эффективен в пространствах большой размерности
- По-прежнему эффективен в случаях, когда количество измерений превышает количество выборок
- Использует подмножество обучающих точек в функции принятия решения, что делает его эффективным с точки зрения памяти
- Различные функции ядра могут быть задана для функции принятия решения, что также делает ее универсальной
- Если количество функций намного больше, чем количество выборок, избегайте чрезмерной подгонки при выборе функций ядра, и термин регуляризации имеет решающее значение. SVM
- не предоставляют напрямую оценки вероятности, они рассчитываются с использованием пятикратной перекрестной проверки.

Основная цель машины опорных векторов состоит в том, чтобы разделить данные наилучшим образом. Когда сегрегация выполнена, расстояние между ближайшими точками называется границей. Подход заключается в выборе гиперплоскости с максимально возможным запасом между опорными векторами в заданных наборах данных.
Чтобы выбрать максимальную гиперплоскость в данных наборах, машина опорных векторов следует следующим наборам:
- Сгенерировать гиперплоскости, которые наилучшим образом разделяют классы
- Выберите правую гиперплоскость с максимальным отделением от ближайших точек данных
В некоторых случаях гиперплоскости не могут быть очень эффективными.В этих случаях машина опорных векторов использует трюк с ядром, чтобы преобразовать ввод в многомерное пространство . Благодаря этому становится легче разделить точки. Давайте посмотрим на ядра SVM.
Ядро SVM в основном добавляет больше измерений к низкоразмерному пространству, чтобы упростить разделение данных. Он преобразует неразрывную проблему в разделимые проблемы, добавляя дополнительные измерения, используя трюк с ядром. Машина опорных векторов на практике реализуется ядром.Уловка с ядром помогает сделать более точный классификатор. Давайте посмотрим на различные ядра в машине опорных векторов.
Он преобразует неразрывную проблему в разделимые проблемы, добавляя дополнительные измерения, используя трюк с ядром. Машина опорных векторов на практике реализуется ядром.Уловка с ядром помогает сделать более точный классификатор. Давайте посмотрим на различные ядра в машине опорных векторов.
Линейное ядро — Линейное ядро может использоваться как нормальный скалярный продукт между любыми двумя данными наблюдениями. Произведение между двумя векторами — это сумма умножения каждой пары входных значений. Ниже приводится уравнение линейного ядра.
Полиномиальное ядро — это довольно обобщенная форма линейного ядра.Он может различать искривленное или нелинейное пространство ввода. Ниже приводится уравнение полиномиального ядра.
Ядро радиальной базисной функции — Ядро радиальной базисной функции обычно используется в классификации SVM, оно может отображать пространство в бесконечных измерениях. Ниже приводится уравнение ядра RBF.
- Распознавание лиц
- Категоризация текста и гипертекста
- Классификация изображений
- Биоинформатика
- Обнаружение протеиновой складки и удаленной гомологии
- Распознавание рукописного ввода
- Обобщенный прогнозный контроль 9
- Загрузка данных
- Исследование данных
- Разделение данных
- Создание модели
- Оценка модели
Мы используем набор данных рака в библиотеке sklearn, мы сделаем классификатор, чтобы предсказать, является ли рак доброкачественным или злокачественным. Мы можем загрузить набор данных следующим образом.
из наборов данных импорта sklearnCance_data = datasets.load_breast_cancer ()
print (Cance_data.data [5]
Результат :
После этого мы исследуем данные. Взглянем на различные значения в наборе данных. Проверьте целевую переменную и т. д.
Взглянем на различные значения в наборе данных. Проверьте целевую переменную и т. д.
Форма означает, что этот набор данных содержит 569 строк и 30 столбцов.
print (Cance_data.data.shape)
#target set
print (Cance_data.target)
Выход :
Здесь 0 представляет злокачественный, а 1 — доброкачественный.
Разделение данныхМы разделим набор данных на обучающий набор и тестовый набор, чтобы получить точные результаты. После этого мы разделим данные с помощью функции train_test_split (). Нам понадобятся 3 параметра, как в примере ниже. Функции для обучения модели, цель и размер тестового набора.
из sklearn.model_selection import train_test_splitСоздание моделиCance_data = datasets.load_breast_cancer ()
X_train, X_test, y_train, y_test = train_test_split (Cance_data.data, Cance_data.target, test_size = 0.4, random_state = 109)
Чтобы сгенерировать модель, мы сначала импортируем модуль SVM из sklearn, чтобы создать классификатор опорных векторов в svc (), передав ядро аргумента как линейное ядро.
Затем мы обучим набор данных с помощью set () и сделаем прогнозы с помощью функции predic ().
из sklearn import svm
# создать классификатор
cls = svm.SVC (kernel = "linear")
# обучить модель
cls.fit (X_train, y_train)
#predict the response
pred = cls.predict (X_test)
Оценка модели
С его помощью мы можем предсказать, насколько точно модель или классификатор может предсказать, есть ли у пациента заболевание сердца или нет. Таким образом, мы рассчитаем оценку точности, отзывчивость и точность для нашей оценки.
из sklearn import metrics
#accuracy
print ("точность:", metrics.accuracy_score (y_test, y_pred = pred))
# оценка точности
print ("precision:", metrics.precision_score (y_test, y_pred = pred))
#recall score
print ("отзыв", metrics.recall_score (y_test, y_pred = pred))
print (metrics.classification_report (y_test, y_pred = pred))
Вывод :
Мы получаем значения точности, точности и отзывчивости как 0,96, 0,96 и 0,97, что маловероятно. Поскольку наш набор данных был достаточно описательным и решающим, мы смогли получить такие точные результаты. Обычно оценка точности выше 0,7 является хорошей оценкой.
Поскольку наш набор данных был достаточно описательным и решающим, мы смогли получить такие точные результаты. Обычно оценка точности выше 0,7 является хорошей оценкой.
Давайте посмотрим на другой пример, чтобы понять, как мы можем использовать алгоритм классификации машины опорных векторов другим способом.
В этом примере мы будем использовать существующий набор цифровых данных и обучить классификатор. После этого мы будем использовать классификатор, чтобы предсказать цифру и сделать изображение более четким.
import matplotlib.pyplot as plt
из наборов данных импорта sklearn
из sklearn import svm
# загрузка набора данных
letter = datasets.load_digits ()
# создание классификатора
clf = svm.SVC (gamma = 0.001, C = 100 )
# обучение классификатора
X, y = letter.data [: - 10], букв.target [: - 10]
clf.fit (X, y)
# прогнозирование вывода
print (clf.predict (letter.data [: - 10]))
plt.imshow (letter.images [6], интерполяция = 'ближайший')
plt.show ()
Выход :
Для повышения точности мы можем изменить значения гаммы или значения C в параметре SVC, но это также снизит скорость. Если мы увеличим значения гаммы, точность уменьшится, но скорость увеличится по сравнению с другими.
Это подводит нас к концу статьи, где мы узнали, как мы можем работать с машинами опорных векторов в Python.Я надеюсь, что вы понимаете все, что было поделено с вами в этом руководстве.
Если вы хотите ознакомиться с дополнительными статьями о самых популярных технологиях на рынке, таких как искусственный интеллект, DevOps, этический взлом, посетите официальный сайт Edureka.
Обязательно обратите внимание на другие статьи в этой серии, которые будут объяснять различные другие аспекты Python и Data Science.
1. Классификатор машинного обучения в Python
2. Шпаргалка по Python Scikit-Learn
3.Инструменты машинного обучения
4.
Библиотеки Python для анализа данных и машинного обучения
5. Чат-бот на Python
6. Коллекции Python
7. Модули Python
8. Навыки разработчика Python
9. ООП Вопросы и ответы на собеседование
10. Резюме для Python-разработчика
11. Исследовательский анализ данных в Python
12. Змейка с модулем Python Turtle
13. Заработная плата разработчика Python
14.Анализ основных компонентов
15. Python против C ++
16. Учебное пособие по Scrapy
17. Python SciPy
18. Метод регрессии наименьших квадратов
19. Шпаргалка по Jupyter Notebook
20. Основы Python
21. Шаблон Python Программы
22. Генераторы на Python
23. Python Decorator
24. Python Spyder IDE
25. Мобильные приложения с использованием Kivy в Python
26. 10 лучших книг для изучения и практики Python
27.Robot Framework с Python
28. Змейка на Python с использованием PyGame
29.
Вопросы и ответы на собеседовании по Django
30. 10 лучших приложений Python
31. Хеш-таблицы и хэш-карты в Python
32. Python 3.8
33 . Python Visual Studio
34. Python Tutorial
Support Vector Machines Tutorial — Научитесь реализовывать SVM в Python
Support Vector Machines Tutorial — Я пытаюсь сделать его всеобъемлющим и интерактивным учебным пособием, чтобы вы могли понять концепции SVM легко.
Несколько дней назад я встретил ребенка, отец которого покупал фрукты у продавца фруктов. Этот ребенок хотел съесть клубнику, но запутался между двумя одинаково выглядящими фруктами. Заметив какое-то время, он понимает, какая из них Strawberry, и выбирает одну из корзины. Как и этот ребенок, машины опорных векторов работают. Он просматривает данные и сортирует их по одной из двух категорий.
Все еще не уверены? Прочтите статью ниже, чтобы подробно разобраться в SVM с множеством примеров.
Введение в машины опорных векторов
SVM — самый популярный алгоритм классификации в алгоритмах машинного обучения . Их математическая подготовка является квинтэссенцией в построении фундаментального блока для геометрического различия между двумя классами. Мы увидим, как работают вспомогательные векторные машины, наблюдая за их реализацией в Python, и, наконец, мы рассмотрим некоторые из важных приложений.
Их математическая подготовка является квинтэссенцией в построении фундаментального блока для геометрического различия между двумя классами. Мы увидим, как работают вспомогательные векторные машины, наблюдая за их реализацией в Python, и, наконец, мы рассмотрим некоторые из важных приложений.
Что такое SVM?
Машины опорных векторов — это тип контролируемого алгоритма машинного обучения, который обеспечивает анализ данных для классификации и регрессионного анализа. Хотя их можно использовать для регрессии, SVM в основном используется для классификации.Строим изображения в n-мерном пространстве. Значение каждой функции также является значением конкретной координаты. Затем мы находим идеальную гиперплоскость, которая различает эти два класса.
Эти опорные векторы являются координатными представлениями индивидуального наблюдения. Это пограничный метод разделения двух классов.
Не забудьте ознакомиться с последним руководством DataFlair по машинному обучению кластеризации
Как работает SVM?
Основной принцип работы опорных векторных машин прост — создайте гиперплоскость, которая разделяет набор данных на классы.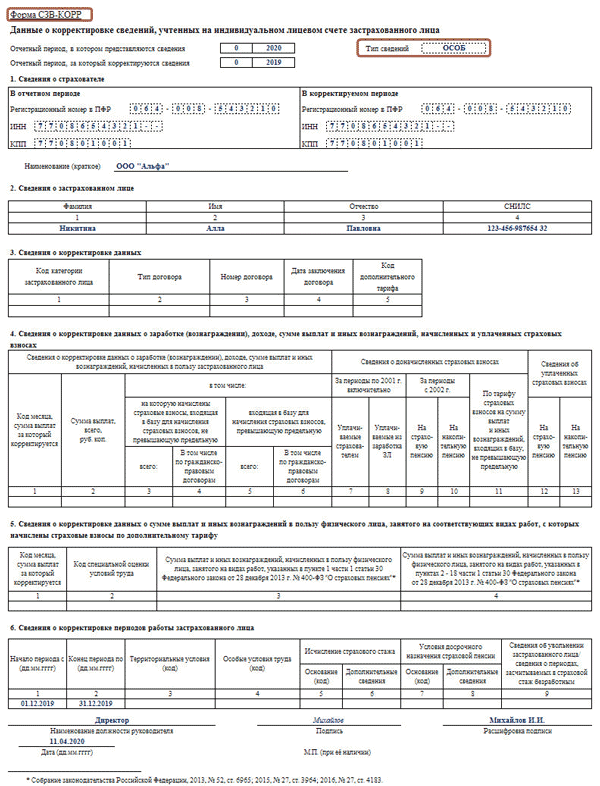 Начнем с примера задачи. Предположим, что для данного набора данных вам нужно классифицировать красные треугольники от синих кругов. Ваша цель — создать линию, которая классифицирует данные на два класса, создавая различие между красными треугольниками и синими кругами.
Начнем с примера задачи. Предположим, что для данного набора данных вам нужно классифицировать красные треугольники от синих кругов. Ваша цель — создать линию, которая классифицирует данные на два класса, создавая различие между красными треугольниками и синими кругами.
Хотя можно выдвинуть гипотезу о четкой линии, разделяющей два класса, может быть много линий, которые могут выполнить эту работу. Следовательно, нет ни одной линии, по которой можно было бы договориться, которая может выполнить эту задачу. Давайте визуализируем некоторые из линий, которые могут различать два класса следующим образом:
В приведенных выше визуализациях у нас есть зеленая линия и красная линия.Как вы думаете, какой из них лучше разделит данные на два класса? Если вы выберете красную линию, то это идеальная линия, которая правильно разделяет два класса. Однако мы до сих пор не конкретизировали тот факт, что это универсальная линия, которая наиболее эффективно классифицирует наши данные.
На этом этапе вы не можете пропустить изучение искусственных нейронных сетей
Зеленая линия не может быть идеальной линией, поскольку она расположена слишком близко к красному классу.Следовательно, он не дает надлежащего обобщения, что является нашей конечной целью.
Согласно SVM, мы должны найти точки, которые находятся ближе всего к обоим классам. Эти точки называются опорными векторами. На следующем этапе мы находим близость между нашей разделяющей плоскостью и опорными векторами. Расстояние между точками и разделительной линией называется полем. Цель алгоритма SVM — максимально увеличить этот запас. Когда запас достигает максимума, гиперплоскость становится оптимальной.
Модель SVM пытается увеличить расстояние между двумя классами путем создания четко определенной границы решения. В приведенном выше случае наша гиперплоскость разделила данные. В то время как наши данные были двухмерными, гиперплоскость была одномерной. Для более высоких измерений, скажем, n-мерного евклидова пространства, у нас есть n-1-мерное подмножество, которое делит пространство на два несвязанных компонента.
Для более высоких измерений, скажем, n-мерного евклидова пространства, у нас есть n-1-мерное подмножество, которое делит пространство на два несвязанных компонента.
Далее в этом руководстве по SVM мы увидим реализацию SVM в Python.Итак, прежде чем двигаться дальше, я рекомендую пересмотреть ваши концепции Python.
Как реализовать SVM в Python?
На первом этапе мы импортируем важные библиотеки, которые мы будем использовать при реализации SVM в нашем проекте.
Код:
импорт панд как pd импортировать numpy как np #DataFlair импортировать matplotlib.pyplot как plt из matplotlib.colors import ListedColormap импортировать matplotlib.pyplot как plt из наборов данных импорта sklearn из склеарна.svm import SVC из sklearn.model_selection import train_test_split из sklearn.preprocessing import StandardScaler % pylab inline
Снимок экрана:
На втором этапе реализации SVM в Python мы будем использовать набор данных iris, доступный с помощью метода load_iris (). В этом анализе мы будем использовать только длину и ширину лепестка.
В этом анализе мы будем использовать только длину и ширину лепестка.
Код:
pylab.rcParams ['figure.figsize'] = (10, 6)
iris_data = наборы данных.load_iris ()
# Мы будем использовать длину и ширину лепестка только для этого анализа
X = iris_data.data [:, [2, 3]]
y = iris_data.target
# Введите данные диафрагмы в фрейм данных pandas
iris_dataframe = pd.DataFrame (iris_data.data [:, [2, 3]],
columns = iris_data.feature_names [2:])
# Просмотр первых 5 строк данных
печать (iris_dataframe.head ())
# Распечатать уникальные метки набора данных
print ('\ n' + 'Уникальные метки, содержащиеся в этих данных:'
+ str (np.unique (y))) Скриншот:
ALERT !! Вы упускаете что-то важное — не забудьте попрактиковаться в последних проектах машинного обучения.Вот один для вас — Обнаружение мошенничества с кредитными картами с использованием машинного обучения
На следующем шаге мы разделим наши данные на обучающий и тестовый набор с помощью функции train_test_split () следующим образом —
Код:
X_train , X_test, y_train, y_test = train_test_split (X, y, test_size = 0.3, random_state = 0) print ('Обучающий набор содержит {} образцов, а тестовый набор содержит {} образцы'.format (X_train.shape [0], X_test.shape [0]))
Скриншот:
Давайте теперь визуализировать наши данные.Заметим, что один из классов линейно отделим.
Код:
маркеры = ('x', 's', 'o')
colors = ('красный', 'синий', 'зеленый')
cmap = ListedColormap (цвета [: len (np.unique (y_test))])
для idx, cl в enumerate (np.unique (y)):
plt.scatter (x = X [y == cl, 0], y = X [y == cl, 1],
c = cmap (idx), marker = markers [idx], label = cl) Снимок экрана:
Вывод:
Затем мы выполним масштабирование наших данных.Масштабирование гарантирует, что все наши значения данных лежат в общем диапазоне, так что не будет крайних значений.
Код:
standard_scaler = StandardScaler () #DataFlair standard_scaler.fit (X_train) X_train_standard = standard_scaler.transform (X_train) X_test_standard = standard_scaler.transform (X_test) print ('Первые пять строк после стандартизации выглядят так: \ n') print (pd.DataFrame (X_train_standard, columns = iris_dataframe.columns) .head ())
Скриншот вывода:
После предварительной обработки данных следующим шагом является реализация модели SVM в виде следует.Мы будем использовать функцию SVC, предоставленную нам библиотекой sklearn. В этом случае мы выберем наше ядро как «rbf».
Код:
#DataFlair
SVM = SVC (ядро = 'rbf', random_state = 0, гамма = .10, C = 1.0)
SVM.fit (X_train_standard, y_train)
print ('Точность нашей модели SVM по обучающим данным составляет {: .2f} из 1'.format (SVM.score (X_train_standard, y_train)))
print ('Точность нашей модели SVM по тестовым данным составляет {: .2f} из 1'.format (SVM.score (X_test_standard, y_test))) Снимок экрана:
Рекомендация DataFlair — Сегментация клиентов с использованием R и машинного обучения
После того, как мы достигли нашей точности, наилучшим способом действий будет визуализация нашей модели SVM.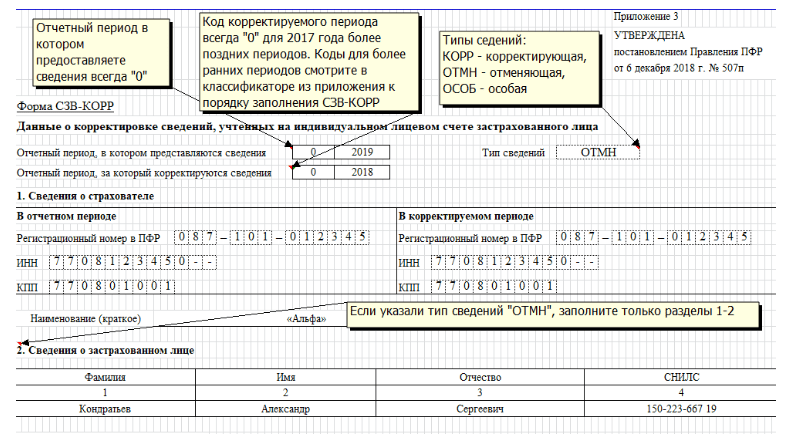 ‘,’ v ‘)
colors = (‘красный’, ‘синий’, ‘зеленый’, ‘серый’, ‘голубой’)
cmap = ListedColormap (цвета [: len (np.unique (y))]) # построить поверхность принятия решений
x1min, x1max = X [:, 0] .min () — 1, X [:, 0] .max () + 1
x2min, x2max = X [:, 1] .min () — 1, X [:, 1] .max () + 1
xx1, xx2 = np.meshgrid (np.arange (x1min, x1max, разрешение),
np.arange (x2min, x2max, разрешение))
Z = classifier.predict (np.array ([xx1.ravel (), xx2.ravel ()]). T)
Z = Z.reshape (xx1.shape)
plt.contourf (xx1, xx2, Z, альфа = 0.4, cmap = cmap)
plt.xlim (xx1.min (), xx1.max ())
plt.ylim (xx2.min (), xx2.max ()) для idx, cl в enumerate (np.unique (y)):
plt.scatter (x = X [y == cl, 0], y = X [y == cl, 1],
альфа = 0,8, c = cmap (idx),
marker = маркеры [idx], label = cl)
‘,’ v ‘)
colors = (‘красный’, ‘синий’, ‘зеленый’, ‘серый’, ‘голубой’)
cmap = ListedColormap (цвета [: len (np.unique (y))]) # построить поверхность принятия решений
x1min, x1max = X [:, 0] .min () — 1, X [:, 0] .max () + 1
x2min, x2max = X [:, 1] .min () — 1, X [:, 1] .max () + 1
xx1, xx2 = np.meshgrid (np.arange (x1min, x1max, разрешение),
np.arange (x2min, x2max, разрешение))
Z = classifier.predict (np.array ([xx1.ravel (), xx2.ravel ()]). T)
Z = Z.reshape (xx1.shape)
plt.contourf (xx1, xx2, Z, альфа = 0.4, cmap = cmap)
plt.xlim (xx1.min (), xx1.max ())
plt.ylim (xx2.min (), xx2.max ()) для idx, cl в enumerate (np.unique (y)):
plt.scatter (x = X [y == cl, 0], y = X [y == cl, 1],
альфа = 0,8, c = cmap (idx),
marker = маркеры [idx], label = cl)
Снимок экрана:
Код:
график решения (X_test_standard, y_test, SVM)
Снимок экрана:
003
00 Сеть 9602 9602 9000 Conolution 9000 — Neural
изучите эту концепцию, чтобы стать экспертомПреимущества и недостатки машины опорных векторов
Преимущества SVM
- Гарантированная оптимальность: благодаря природе выпуклой оптимизации решение всегда будет глобальным минимумом, а не локальным минимумом.

- Изобилие реализаций: мы можем получить к нему удобный доступ, будь то из Python или Matlab.
- SVM может использоваться как для линейно разделимых, так и для нелинейно разделимых данных. Линейно разделяемые данные представляют собой жесткую границу, тогда как нелинейно разделяемые данные представляют собой мягкую границу. SVM
- обеспечивают соответствие моделям полууправляемого обучения. Его можно использовать в областях, где данные помечены, а также не помечены. Это требует только условия для задачи минимизации, которая известна как Transductive SVM.
- Отображение функций раньше сильно влияло на вычислительную сложность общей обучающей производительности модели. Однако с помощью Kernel Trick SVM может выполнять отображение функций с помощью простого скалярного произведения.
Недостатки SVM
- SVM не может обрабатывать текстовые структуры. Это приводит к потере последовательной информации и, следовательно, к снижению производительности.

- Vanilla SVM не может вернуть значение вероятностной достоверности, подобное логистической регрессии.Это не дает подробного объяснения, поскольку уверенность в предсказании важна в нескольких приложениях.
- Выбор ядра — это, пожалуй, самое большое ограничение машины опорных векторов. Принимая во внимание такое количество ядер, трудно выбрать подходящее для данных.
Узнайте все о рекуррентных нейронных сетях и их приложениях
Как настроить параметры SVM?
Ядро
Ядро в SVM отвечает за преобразование входных данных в требуемый формат.Некоторые из ядер, используемых в SVM, являются линейными, полиномиальными и радиальными базисными функциями (RBF). Для создания нелинейной гиперплоскости мы используем RBF и полиномиальную функцию. Для сложных приложений следует использовать более продвинутые ядра для разделения классов, которые являются нелинейными по своей природе. С помощью этого преобразования можно получить точные классификаторы.
Регуляризация
Мы можем поддерживать регуляризацию, настраивая ее в параметрах C. Scikit-learn. C обозначает параметр штрафа, представляющий ошибку или любую форму неправильной классификации.С этой ошибочной классификацией можно понять, какая часть ошибки действительно допустима. Благодаря этому вы можете свести на нет компенсацию между неправильно классифицированным термином и границей решения. С меньшим значением C мы получаем гиперплоскость с малым запасом, а с большим значением C мы получаем гиперплоскость с большим значением.
Gamma
При более низком значении Gamma будет создаваться неплотное соответствие обучающего набора данных. Напротив, высокое значение гаммы позволит модели более точно подогнать под себя.Низкое значение гаммы учитывает только близлежащие точки для расчета отдельной плоскости, тогда как высокое значение гаммы учитывает все точки данных для расчета окончательной линии разделения.
Приложения SVM
Некоторые из областей, в которых используются машины опорных векторов, следующие:
SVM способны классифицировать изображения людей в окружающей среде, создавая квадратную рамку, отделяющую лицо от остальных.
Категоризация текста и гипертекста
SVM могут использоваться для классификации документов в том смысле, что они выполняют категоризацию текста и гипертекста.На основе полученной оценки выполняется сравнение с пороговым значением.
В области биоинформатики SVM используются для классификации белков и геномной классификации. Они могут классифицировать генетическую структуру пациентов на основе их биологических проблем.
Еще одна область, в которой машины опорных векторов используются для визуального распознавания, — это распознавание рукописного ввода.
Резюме
В этой статье мы узнали о машинах опорных векторов. Мы узнали, как работают эти алгоритмы SVM, а также реализовали их на реальном примере.Мы также обсудили различные применения SVM в нашей повседневной жизни. Надеюсь, теперь вы понимаете всю теорию SVM.
Чему вы хотите научиться дальше? Комментарий ниже. DataFlair вам обязательно поможет.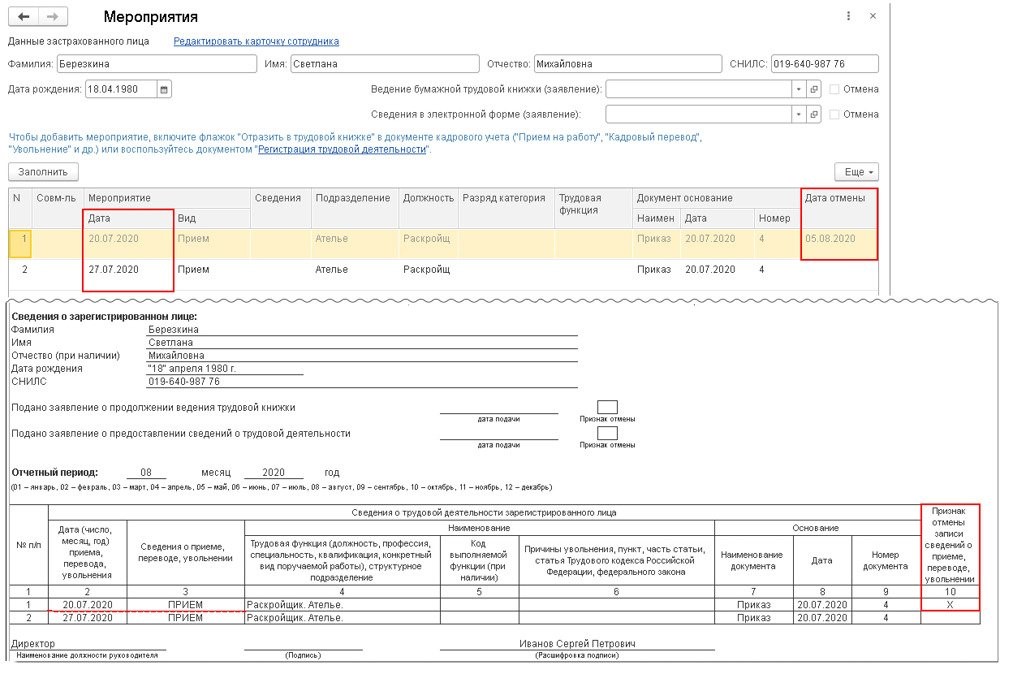
А пока продолжайте изучать руководства по машинному обучению. Счастливое обучение 😊
Модель машины опорных векторов для ингибирующих действий hERG на основе интегрированной базы данных hERG с использованием выбора дескриптора с помощью NSGA-II
Выбор дескриптора
Результат выбора дескриптора с помощью NSGA-II показан на рис.1. Коэффициент доминирования описывает соотношение решений Парето поколения i-1, в котором преобладают решения Парето поколения i. После 80-го поколения коэффициент доминирования меньше 0,1, что означает, что большинство решений Парето не обновлялись (рис. 1 (а)). Таким образом, 100 поколений будет достаточно для оптимизации двух объективных показателей. Среди 40 решений Парето в 100-м поколении набор дескрипторов с 35 дескрипторами показал хорошо сбалансированную производительность прогнозирования (точность = 0.870, Каппа = 0,741). С большим количеством дескрипторов каппа CV показала лишь небольшое улучшение по сравнению с теми, которые использовали 35 дескрипторов (рис. 1 (b)).
1 (b)).
Наборы дескрипторов решений Парето в сотом поколении были объединены с ECFP_4. По сравнению с одним ECFP_4, комбинация наборов дескрипторов и ECFP_4 зафиксировала улучшенную статистику каппа (рис. 1 (c)). Как и в случае моделей SVM, использующих только дескрипторы, производительность прогнозирования немного улучшилась, когда больше дескрипторов было объединено с ECFP_4.Затем было проведено дополнительное исследование, чтобы подтвердить баланс между количеством дескрипторов и производительностью прогнозирования. Из решений Парето в сочетании с ECFP_4 из диапазона каждых 10 дескрипторов был выбран набор дескрипторов, показывающий наивысшее значение CV каппа. Путем исключения наборов дескрипторов, показывающих более низкие значения каппа CV, чем те, которые используют меньшее количество дескрипторов, пять наборов дескрипторов (10, 20, 28, 60 и 72 дескриптора, выделенные на рис. 1 (c)) были выбраны для построения модели с использованием всех обучающих данных. .Статистика перекрестной проверки с помощью моделей прогнозирования, построенных с помощью пяти наборов дескрипторов, показана в таблице 3. Все модели показали достаточную производительность прогнозирования. Среди пяти моделей модель с 72 дескрипторами показала наилучшую производительность (точность = 0,983, сбалансированная точность = 0,854, каппа = 0,735), и выбранные дескрипторы, по-видимому, соответствовали характеристикам ингибиторов hERG, о которых сообщалось в предыдущем исследовании 36 .
Все модели показали достаточную производительность прогнозирования. Среди пяти моделей модель с 72 дескрипторами показала наилучшую производительность (точность = 0,983, сбалансированная точность = 0,854, каппа = 0,735), и выбранные дескрипторы, по-видимому, соответствовали характеристикам ингибиторов hERG, о которых сообщалось в предыдущем исследовании 36 .
Точность и каппа CV модели, объединяющей ECFP_4 и все вычисленные 424 дескриптора, составляли 0,901 и 0,714, в то время как те из комбинации ECFP_4 с 212 дескрипторами, наибольшим набором дескрипторов, оцененным при выборе дескрипторов NSGA-II, были 0,983 и 0,728 соответственно. При сравнении этих двух моделей модель по выбору дескрипторов показала несколько более высокую прогностическую эффективность при меньшем количестве дескрипторов. Этот результат показал, что сложность модели была уменьшена за счет удаления избыточных и нерелевантных дескрипторов. Поэтому модель SVM, основанная на дескрипторах ECFP_4 и 72, была выбрана в качестве набора дескрипторов с хорошим балансом между количеством дескрипторов и предсказательной эффективностью. 72 выбранных дескриптора перечислены в дополнительной таблице S2.
Поэтому модель SVM, основанная на дескрипторах ECFP_4 и 72, была выбрана в качестве набора дескрипторов с хорошим балансом между количеством дескрипторов и предсказательной эффективностью. 72 выбранных дескриптора перечислены в дополнительной таблице S2.
Оценка выбранных дескрипторов
Важность каждого молекулярного дескриптора оценивалась по количеству вхождений в 40 растворов Парето в последнем поколении. Часто используемые молекулярные дескрипторы можно рассматривать как важные дескрипторы для ингибирования hERG.Частота каждого дескриптора показана на рисунке 2.
Рисунок 2Частота дескрипторов в сотом поколении решений Парето.
Согласно анализу сайт-направленного мутагенеза и моделированию гомологии 37,38,39 , Tyr652 и Phe656 были идентифицированы как важные остатки, образующие электростатические взаимодействия (катион-π) и взаимодействия π-укладки с несколькими известными ингибиторами hERG. Наиболее часто выбираемый дескриптор — AM1_HOMO, который может представлять электростатические условия в ароматическом кольце и коррелирует π-π взаимодействие с Phe656. Второй — pKa, который может представлять π-взаимодействие катиона с Tyr652. Фактически, многие ингибиторы hERG имеют ароматическое кольцо в конце лиганда и основной амин, который легко протонируется при физиологическом pH. В нашем предыдущем исследовании, хотя около 80% неактивных соединений не имели положительно заряженных атомов, более половины ингибиторов hERG содержали по крайней мере один положительно заряженный атом. Поэтому при выборе дескрипторов также были выбраны дескрипторы, связанные с атомным зарядом, такие как PEOE_VSA_plus, GCUT_PEOE и PC_plus.
Второй — pKa, который может представлять π-взаимодействие катиона с Tyr652. Фактически, многие ингибиторы hERG имеют ароматическое кольцо в конце лиганда и основной амин, который легко протонируется при физиологическом pH. В нашем предыдущем исследовании, хотя около 80% неактивных соединений не имели положительно заряженных атомов, более половины ингибиторов hERG содержали по крайней мере один положительно заряженный атом. Поэтому при выборе дескрипторов также были выбраны дескрипторы, связанные с атомным зарядом, такие как PEOE_VSA_plus, GCUT_PEOE и PC_plus.
Помимо атомного заряда, в нескольких предыдущих исследованиях сообщалось, что соединения, отвечающие за hERG, имеют тенденцию быть больше, более гидрофобными, более гибкими и имеют меньше акцепторов Н-связи 36,40 . Размер молекулы был выражен диаметром, и в наших моделях использовались дескрипторы на основе молекулярной рефракции SMR_VSA и SMR_VSA. Гидрофобность была выражена дескрипторами на основе logP, такими как logD, logP (o / w) и SlogP_VSA.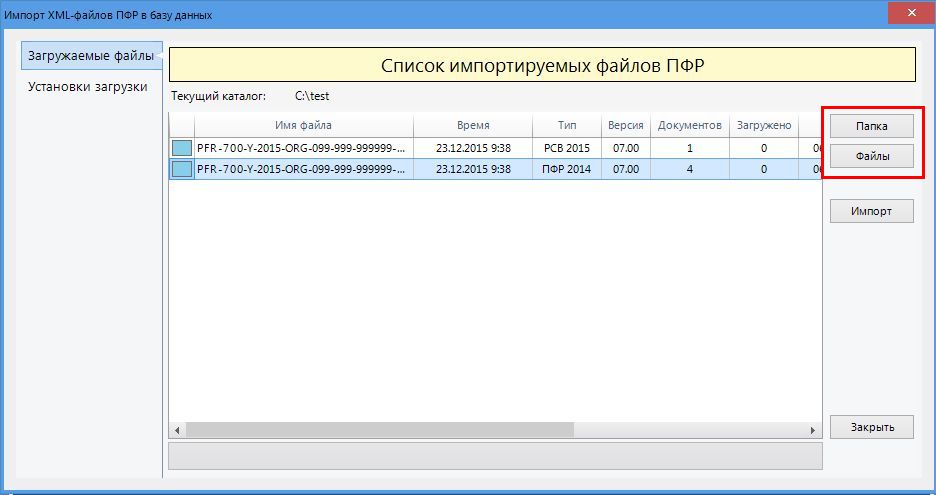 Гидрофобность также связана с площадью полярной поверхности, поэтому была выбрана также Molecular_Fractional_PolarSurfaceArea.Эти дескрипторы могут быть объяснены гидрофобной природой поровой области hERG из-за большого количества гидрофобных аминокислот. Таким образом, эффективность обычно увеличивается с увеличением logP лиганда.
Гидрофобность также связана с площадью полярной поверхности, поэтому была выбрана также Molecular_Fractional_PolarSurfaceArea.Эти дескрипторы могут быть объяснены гидрофобной природой поровой области hERG из-за большого количества гидрофобных аминокислот. Таким образом, эффективность обычно увеличивается с увеличением logP лиганда.
Молекулярная гибкость была представлена Num_Aliphatic SingleBonds, b_bond, Num_Doublebond и opr_brigid, которые показывают жесткость молекул. Были включены два дескриптора, относящиеся к количеству двойных связей. Num_DoubleBonds подсчитывает количество всех двойных связей, а b_double подсчитывает количество двойных связей, исключая те, что находятся в ароматических кольцах.Большинство лигандов, которые показали сильную активность в отношении hERG, имеют азотсодержащие алкильные цепи 41 , и гибкость может рассматриваться как важная особенность ингибирования hERG.
Некоторые фармакофорные модели 42 и мутационный анализ показали, что водородные связи с Thr623, Ser624 и Val625 играют важную роль в ингибировании hERG. Характеристики акцепторов водородной связи (vsa_acc, a_acc и Num_H_Acceptors) были выбраны NSGA-II. В целом, эти часто выбираемые дескрипторы, по-видимому, соответствовали характеристикам ингибитора hERG, о которых сообщалось в предыдущих исследованиях.
Характеристики акцепторов водородной связи (vsa_acc, a_acc и Num_H_Acceptors) были выбраны NSGA-II. В целом, эти часто выбираемые дескрипторы, по-видимому, соответствовали характеристикам ингибитора hERG, о которых сообщалось в предыдущих исследованиях.
Интеграция баз данных
Из-за неоднородности протоколов анализа на ингибирование hERG построение модели прогнозирования с использованием нескольких баз данных может нарушить согласованность данных и, возможно, привести к риску снижения производительности прогнозирования. Таким образом, была оценена адекватность использования интегрированного набора данных hERG для построения модели прогнозирования. Чтобы исследовать взаимосвязь между производительностью прогнозирования и источниками данных, обучающий набор и тестовый набор были разделены исходной базой данных каждой записи анализа для компиляции наборов данных, соответствующих отдельным базам данных.Затем построение модели SVM и оценка производительности прогнозирования на основе оценок ROC были выполнены для всех комбинаций обучающего набора и тестового набора. Сравнение проводилось для моделей SVM с использованием ECFP4 для исследования эффекта интеграции данных (рис. 3 (a)) и моделей SVM с использованием ECFP4 с 72 дескрипторами, выбранными NSGA-II (рис. 3 (b)) для оценки тех, которые после выбор дескриптора. Как сообщалось ранее 23 , соединения в ChEMBL и GOSTAR, составленные из литературных источников и патентов, имели другое распределение молекулярных свойств и соотношение ингибиторов hERG к неактивным соединениям по сравнению с соединениями в NCGC и hERGCentral, составленных на основе результатов HTS. химических библиотек.В результате модели SVM, построенные из отдельных баз данных, не смогли обеспечить высокую производительность прогнозирования для набора тестов, скомпилированного из разных баз данных.
Сравнение проводилось для моделей SVM с использованием ECFP4 для исследования эффекта интеграции данных (рис. 3 (a)) и моделей SVM с использованием ECFP4 с 72 дескрипторами, выбранными NSGA-II (рис. 3 (b)) для оценки тех, которые после выбор дескриптора. Как сообщалось ранее 23 , соединения в ChEMBL и GOSTAR, составленные из литературных источников и патентов, имели другое распределение молекулярных свойств и соотношение ингибиторов hERG к неактивным соединениям по сравнению с соединениями в NCGC и hERGCentral, составленных на основе результатов HTS. химических библиотек.В результате модели SVM, построенные из отдельных баз данных, не смогли обеспечить высокую производительность прогнозирования для набора тестов, скомпилированного из разных баз данных.
Оценки ROC моделей SVM, построенных на основе интегрированной базы данных hERG (голубая полоса), ChEMBL (синяя линия), GOSTAR (красная линия), NCGC (зеленая линия) и hERGCentral (фиолетовая линия), используя дескрипторы ( a ) ECFP4, ( b ) ECFP4 и 72 в качестве независимых переменных. Горизонтальная ось соответствует источнику данных тестового набора.
Горизонтальная ось соответствует источнику данных тестового набора.
Для моделей SVM, использующих ECFP4, средний балл ROC составлял 0,694, когда модель обучалась с помощью обучающего набора, полученного из другой базы данных для тестового набора, и 0,870, когда обучающий набор и тестовый набор были получены из одного и того же набора. база данных. Поскольку hERGCentral был составлен из HTS почти 300 000 соединений в репозитории малых молекул молекулярной библиотеки Национального института здравоохранения США, соответствующий набор тестов может быть наилучшим приближением к реальной ситуации HTS.Для сборки тестового набора от hERGCentral все оценки ROC для моделей SVM, созданных ChEMBL, GOSTAR и NCGC, были ниже 0,75. Поскольку количество неактивных соединений hERG в ChEMBL, GOSTAR и NCGC было намного меньше, чем в hERGCentral (таблица 1), эти три модели прогнозирования не могли иметь дело со структурно разнородными соединениями в наборе данных hERGCentral. Оценки ROC модели SVM, построенной из интегрированного набора данных hERG, показали почти эквивалентные оценки ROC по сравнению с моделями SVM, построенными из соответствующих обучающих наборов (0. 864 для ChEMBL, 0,880 для GOSTAR, 0,846 для NCGC и 0,912 для hERG Central), что указывает на то, что интеграция разнородных записей анализа вызвала небольшой отрицательный эффект на производительность прогнозирования и обеспечила лучший охват химического пространства для улучшенной применимости.
864 для ChEMBL, 0,880 для GOSTAR, 0,846 для NCGC и 0,912 для hERG Central), что указывает на то, что интеграция разнородных записей анализа вызвала небольшой отрицательный эффект на производительность прогнозирования и обеспечила лучший охват химического пространства для улучшенной применимости.
В аспекте выбора дескриптора с использованием NSGA-II оценки ROC были последовательно улучшены путем добавления 72 дескрипторов по сравнению с моделями SVM, использующими только ECFP_4 для всех комбинаций обучающих наборов и наборов тестов, что указывает на то, что дескриптор отбор смог успешно получить основные свойства ингибиторов hERG в различных базах данных.Подробные данные оценок ROC были доступны во вспомогательной информации (таблица S3) вместе с соответствующей статистикой Каппа.
Прогнозирование построенной модели SVM по сравнению с коммерческим программным обеспечением
Тестовый набор из 87 361 молекулы использовался для проверки построенной модели SVM и коммерческих приложений. Характеристики прогнозирования для тестового набора показаны в таблице 4. Модель SVM достигла статистики каппа 0,733 с точностью 0,984, чувствительностью 0.670 и специфичность 0,995. Значение статистики каппа было эквивалентно значению перекрестной проверки (0,735). Эти результаты показали устойчивость нашей модели к переобучению.
Характеристики прогнозирования для тестового набора показаны в таблице 4. Модель SVM достигла статистики каппа 0,733 с точностью 0,984, чувствительностью 0.670 и специфичность 0,995. Значение статистики каппа было эквивалентно значению перекрестной проверки (0,735). Эти результаты показали устойчивость нашей модели к переобучению.
Затем эффективность прогнозирования сравнивалась с результатами, полученными с помощью коммерческих моделей (ACD / Percepta, ADMET Predictor и StarDrop). Для сравнения соединения, которые нельзя предсказать с помощью некоторых коммерческих моделей, были удалены из набора для испытаний, и все модели были проверены с использованием 77 062 соединений.Результаты показаны в Таблице 4. Среди трех коммерческих моделей ACD / Percepta продемонстрировала лучшую прогностическую эффективность со статистикой каппа 0,304, точностью 0,905, чувствительностью 0,702 и специфичностью 0,912. ADMET Predictor и StarDrop зафиксировали плохую статистику каппа менее 0,1. В таблице 4 площадь под кривой ROC (ROC_AUC) также была предоставлена в качестве еще одного показателя для оценки эффективности классификации. Значение ROC_AUC не зависит от порога классификации и может оценивать способность классификатора к ранжированию.Для визуализации качества ранжирования кривая ROC показана на рис. 4. При оценке ROC_AUC коммерческие модели показали хорошие результаты (0,831–0,890), что указывает на то, что все коммерческое программное обеспечение хорошо работало при ранжировании ингибирующей активности. . Учитывая, что и ADMET Predictor, и StarDrop также зарегистрировали умеренно высокие показатели ROC 0,866 и 0,831, низкая статистика каппа этих двух регрессионных моделей не подходила для использования дискриминации при критерии IC 50 = 10 мкМ.При сравнении с построенной моделью наша модель показала самый высокий ROC_AUC, равный 0,966, со значением каппа 0,749 и точностью 0,985.
ADMET Predictor и StarDrop зафиксировали плохую статистику каппа менее 0,1. В таблице 4 площадь под кривой ROC (ROC_AUC) также была предоставлена в качестве еще одного показателя для оценки эффективности классификации. Значение ROC_AUC не зависит от порога классификации и может оценивать способность классификатора к ранжированию.Для визуализации качества ранжирования кривая ROC показана на рис. 4. При оценке ROC_AUC коммерческие модели показали хорошие результаты (0,831–0,890), что указывает на то, что все коммерческое программное обеспечение хорошо работало при ранжировании ингибирующей активности. . Учитывая, что и ADMET Predictor, и StarDrop также зарегистрировали умеренно высокие показатели ROC 0,866 и 0,831, низкая статистика каппа этих двух регрессионных моделей не подходила для использования дискриминации при критерии IC 50 = 10 мкМ.При сравнении с построенной моделью наша модель показала самый высокий ROC_AUC, равный 0,966, со значением каппа 0,749 и точностью 0,985. Наша модель явно превзошла коммерческие модели. Относительно низкая чувствительность модели могла быть вызвана использованием данных hERGCentral. Как показано в Таблице 1, результаты HTS в hERGCentral содержат огромное количество неактивных соединений и, таким образом, резко снизили соотношение положительных образцов в наборе данных. Это несбалансированное количество положительных и отрицательных примеров может сместить порог модели в сторону отрицательного предсказания.Тем не менее, более высокая кривая ROC на рис. 4 показывает, что модель SVM различает ингибиторы hERG явно более эффективные, чем коммерческие модели, и баланс положительного и отрицательного прогноза может быть откалиброван путем установки порогового значения, когда это необходимо. Интеграция нескольких баз данных значительно увеличила информацию об ингибировании hERG, что способствовало повышению производительности прогнозирования. В частности, наша модель показала более высокую точность (0,849) по сравнению с коммерческими моделями (0.
Наша модель явно превзошла коммерческие модели. Относительно низкая чувствительность модели могла быть вызвана использованием данных hERGCentral. Как показано в Таблице 1, результаты HTS в hERGCentral содержат огромное количество неактивных соединений и, таким образом, резко снизили соотношение положительных образцов в наборе данных. Это несбалансированное количество положительных и отрицательных примеров может сместить порог модели в сторону отрицательного предсказания.Тем не менее, более высокая кривая ROC на рис. 4 показывает, что модель SVM различает ингибиторы hERG явно более эффективные, чем коммерческие модели, и баланс положительного и отрицательного прогноза может быть откалиброван путем установки порогового значения, когда это необходимо. Интеграция нескольких баз данных значительно увеличила информацию об ингибировании hERG, что способствовало повышению производительности прогнозирования. В частности, наша модель показала более высокую точность (0,849) по сравнению с коммерческими моделями (0. 066–0.225). Точность — это скорость, с которой соединение, согласно прогнозам, является положительным, на самом деле является ингибитором hERG. Коммерческое программное обеспечение, как правило, предсказывало больше ложных срабатываний, указывающих на переоценку риска hERG неактивных соединений. Среди коммерческого программного обеспечения ACD Percepta показала более высокую специфичность к ADMET Predictor и StarDrop. Поскольку ADMET Predictor и StarDrop были созданы для обеспечения регрессионной модели для предсказания hERG K и , их набор данных состоял из соединений, для которых их аффинность связывания с hERG могла быть количественно определена, что означает, что неактивные соединения, не проявляющие никакой ингибирующей активности hERG, не могли быть включены, и возможно, что приведет к снижению точности прогноза для неактивных соединений.Результаты показали эффективность моделей дискриминации для проверки исходных результатов HTS, которые распространяются в более широком химическом пространстве.
066–0.225). Точность — это скорость, с которой соединение, согласно прогнозам, является положительным, на самом деле является ингибитором hERG. Коммерческое программное обеспечение, как правило, предсказывало больше ложных срабатываний, указывающих на переоценку риска hERG неактивных соединений. Среди коммерческого программного обеспечения ACD Percepta показала более высокую специфичность к ADMET Predictor и StarDrop. Поскольку ADMET Predictor и StarDrop были созданы для обеспечения регрессионной модели для предсказания hERG K и , их набор данных состоял из соединений, для которых их аффинность связывания с hERG могла быть количественно определена, что означает, что неактивные соединения, не проявляющие никакой ингибирующей активности hERG, не могли быть включены, и возможно, что приведет к снижению точности прогноза для неактивных соединений.Результаты показали эффективность моделей дискриминации для проверки исходных результатов HTS, которые распространяются в более широком химическом пространстве. Модели регрессии следует рассматривать на более поздней стадии, когда ингибирующая активность hERG определенного хитового соединения должна быть изменена посредством химического синтеза. Наша модель может быть полезна на ранней стадии программы открытия лекарств, такой как сортировка HTS, когда целью является удаление соединений с высокой вероятностью ингибирования hERG.
Модели регрессии следует рассматривать на более поздней стадии, когда ингибирующая активность hERG определенного хитового соединения должна быть изменена посредством химического синтеза. Наша модель может быть полезна на ранней стадии программы открытия лекарств, такой как сортировка HTS, когда целью является удаление соединений с высокой вероятностью ингибирования hERG.
Кривая ROC модели SVM с использованием 72 дескрипторов и ECFP_4 (красный) по сравнению с ACD / Percepta (оранжевый), ADMET Predictor (синий) и StarDrop (зеленый).
Поскольку коммерческие модели демонстрируют низкую специфичность, 4298 неактивных соединений были ошибочно классифицированы как ингибиторы hERG всеми тремя коммерческими моделями. Среди 4298 ложноположительных случаев 4162 соединения были правильно предсказаны как неактивные с помощью нашей модели SVM. Большинство этих ложноположительных соединений имели алифатический атом азота в центре молекулярной структуры. Хотя хорошо известно, что π-взаимодействия положительно заряженных атомов важны для связывания hERG, взаимодействия между атомами азота, содержащимися в неправильно классифицированных ложноположительных соединениях, и hERG кажутся сложными по следующим причинам: (1) влияние окружающей среды. объемные заместители вокруг атома азота и (2) атом азота обычно не заряжен положительно из-за присоединенных электроноакцепторных групп.Кроме того, в ложноположительных результатах также наблюдались неактивные соединения, которые разделяют тот же каркас с ингибиторами hERG, но не имеют ключевого атома азота или ароматического кольца. На рисунке 5 показаны типичные примеры неактивных соединений, которые правильно предсказала только наша модель SVM, вместе с их наиболее похожими ингибиторами hERG. Наша модель SVM успешно предсказала все пары ингибитор / неактивный, в то время как ни одна из трех коммерческих программ не смогла различить неактивные соединения. В случаях на рис.5 (а, б) положительно заряженные атомы азота в hERG были модифицированы в неактивные соединения.
Хотя хорошо известно, что π-взаимодействия положительно заряженных атомов важны для связывания hERG, взаимодействия между атомами азота, содержащимися в неправильно классифицированных ложноположительных соединениях, и hERG кажутся сложными по следующим причинам: (1) влияние окружающей среды. объемные заместители вокруг атома азота и (2) атом азота обычно не заряжен положительно из-за присоединенных электроноакцепторных групп.Кроме того, в ложноположительных результатах также наблюдались неактивные соединения, которые разделяют тот же каркас с ингибиторами hERG, но не имеют ключевого атома азота или ароматического кольца. На рисунке 5 показаны типичные примеры неактивных соединений, которые правильно предсказала только наша модель SVM, вместе с их наиболее похожими ингибиторами hERG. Наша модель SVM успешно предсказала все пары ингибитор / неактивный, в то время как ни одна из трех коммерческих программ не смогла различить неактивные соединения. В случаях на рис.5 (а, б) положительно заряженные атомы азота в hERG были модифицированы в неактивные соединения. Фиг.5 (c, d) представляют случаи, в которых модификации изменяли тенденцию к ионизации атомов азота в пиперазиновых кольцах. На рис. 5 (e) объемная химическая группа может вызвать стерическое столкновение с hERG. На рис. 5 (f) исчезновение концевого ароматического кольца могло ослабить аффинность связывания с hERG. Присутствие двух ароматических колец рядом с положительно заряженным атомом азота является одним из хорошо известных фармакофоров для связывания hERG, и считается, что ароматические кольца образуют π-электронные взаимодействия с Tyr652 и Phe654 hERG.В коммерческих моделях ингибирующая активность соединений с такими недоступными или незаряженными атомами азота имела тенденцию переоцениваться. Успешное различение с помощью нашей модели SVM различий в ингибировании hERG с помощью таких подробных структурных изменений может быть улучшено за счет увеличения обучающих данных в интегрированном наборе данных. Эта улучшенная специфичность предсказания была бы особенно полезной в случае, когда структурная модификация, чтобы избежать ингибирования hERG, необходима в процессе оптимизации попадания, чтобы вести вперед.
Фиг.5 (c, d) представляют случаи, в которых модификации изменяли тенденцию к ионизации атомов азота в пиперазиновых кольцах. На рис. 5 (e) объемная химическая группа может вызвать стерическое столкновение с hERG. На рис. 5 (f) исчезновение концевого ароматического кольца могло ослабить аффинность связывания с hERG. Присутствие двух ароматических колец рядом с положительно заряженным атомом азота является одним из хорошо известных фармакофоров для связывания hERG, и считается, что ароматические кольца образуют π-электронные взаимодействия с Tyr652 и Phe654 hERG.В коммерческих моделях ингибирующая активность соединений с такими недоступными или незаряженными атомами азота имела тенденцию переоцениваться. Успешное различение с помощью нашей модели SVM различий в ингибировании hERG с помощью таких подробных структурных изменений может быть улучшено за счет увеличения обучающих данных в интегрированном наборе данных. Эта улучшенная специфичность предсказания была бы особенно полезной в случае, когда структурная модификация, чтобы избежать ингибирования hERG, необходима в процессе оптимизации попадания, чтобы вести вперед.
Соединения, для которых только модель SVM правильно предсказала активность, и их наиболее похожие ингибиторы hERG. Каждая структура была ионизирована при pH 7,4.
Область применимости
Для оценки области применимости модели классификации для надежного прогнозирования была исследована взаимосвязь между сходством тестируемых соединений с обучающими соединениями и характеристиками прогнозирования. В то время как среднее значение ближайшего сходства Танимото соединений тестового набора с их ближайшими обучающими соединениями было равно 0.726, более половины тестируемых соединений имели структурно похожие соединения в обучающей выборке. Как показано на рис. 6, соединения с высоким сходством с обучающей выборкой показали более высокую точность предсказания. Однако снижение чувствительности и увеличение количества ложноотрицательных соединений наблюдались для соединений с меньшим сходством, за исключением диапазона значений сходства от 0,1 до 0,2.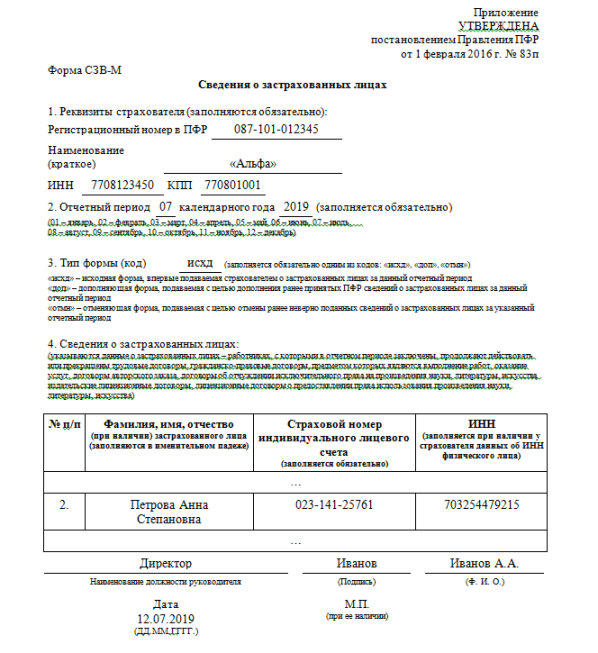 Поскольку количество соединений со значениями сходства 0,1–0,3 было относительно небольшим и содержало только 9 ингибиторов hERG и 86 неактивных соединений, повышение предсказательной способности, наблюдаемое в области низкого сходства, не казалось статистически значимым.Эти результаты позволили понять область применимости модели для надежного прогноза. Хотя на специфичность не повлияло уменьшение сходства по Танимото, чувствительность упала ниже 0,5, когда сходство по Танимото было ниже 0,6, что привело к низкой надежности для отрицательных прогнозов. Принимая во внимание предыдущие отчеты, предполагающие, что соединения со значением сходства 0,6 или выше, как правило, проявляют аналогичную активность 43,44 , пороговое значение 0.6 для критериев области применимости. Путем определения тестируемых соединений со сходством ниже 0,6 за пределами области применимости 12 519 соединений из 87 361 соединения из набора для испытаний были классифицированы как находящиеся вне области применимости.
Поскольку количество соединений со значениями сходства 0,1–0,3 было относительно небольшим и содержало только 9 ингибиторов hERG и 86 неактивных соединений, повышение предсказательной способности, наблюдаемое в области низкого сходства, не казалось статистически значимым.Эти результаты позволили понять область применимости модели для надежного прогноза. Хотя на специфичность не повлияло уменьшение сходства по Танимото, чувствительность упала ниже 0,5, когда сходство по Танимото было ниже 0,6, что привело к низкой надежности для отрицательных прогнозов. Принимая во внимание предыдущие отчеты, предполагающие, что соединения со значением сходства 0,6 или выше, как правило, проявляют аналогичную активность 43,44 , пороговое значение 0.6 для критериев области применимости. Путем определения тестируемых соединений со сходством ниже 0,6 за пределами области применимости 12 519 соединений из 87 361 соединения из набора для испытаний были классифицированы как находящиеся вне области применимости. Хотя каппа-статистика для соединений за пределами области применимости все еще была довольно высокой (0,512), наблюдалась значительная деградация по сравнению с таковой в области применимости (каппа-статистика = 0,762). Низкая чувствительность 0.392 для внешних соединений предположил, что модель имеет тенденцию предоставлять отрицательные прогнозы для соединений, которые не похожи на какие-либо соединения в обучающей выборке, что содержит потенциальный риск ложноотрицательных результатов. Тем не менее, поскольку ранее представленный анализ интегрированной базы данных показал ее более высокое структурное разнообразие, охватывающее 18,2% каркасов Murcko, обнаруженных в базе данных ChEMBL, и содержащих ингибиторы hERG с более чем вдвое большим количеством каркасов Murcko, чем в других базах данных 23 ожидается, что наша модель будет охватывать значительный объем химического пространства, что позволит точно прогнозировать различные лекарственные соединения, включая недавно разработанные.
Хотя каппа-статистика для соединений за пределами области применимости все еще была довольно высокой (0,512), наблюдалась значительная деградация по сравнению с таковой в области применимости (каппа-статистика = 0,762). Низкая чувствительность 0.392 для внешних соединений предположил, что модель имеет тенденцию предоставлять отрицательные прогнозы для соединений, которые не похожи на какие-либо соединения в обучающей выборке, что содержит потенциальный риск ложноотрицательных результатов. Тем не менее, поскольку ранее представленный анализ интегрированной базы данных показал ее более высокое структурное разнообразие, охватывающее 18,2% каркасов Murcko, обнаруженных в базе данных ChEMBL, и содержащих ингибиторы hERG с более чем вдвое большим количеством каркасов Murcko, чем в других базах данных 23 ожидается, что наша модель будет охватывать значительный объем химического пространства, что позволит точно прогнозировать различные лекарственные соединения, включая недавно разработанные. Подробные данные были доступны в вспомогательной информационной таблице S4.
Подробные данные были доступны в вспомогательной информационной таблице S4.
Показатели производительности для набора тестов в каждом диапазоне сходства. Горизонтальная ось обозначает диапазон сходства, а вертикальная ось указывает значения точности (красный), сбалансированной точности (охра), каппа (зеленый), чувствительности (синий) и специфичности (зеленый).
Границы | Машина опорных векторов для анализа вкладов областей мозга во время состояния задачи fMRI
Введение
В анализе данных функционального магнитного резонанса GLM (обобщенные линейные модели) являются одним из наиболее распространенных методов, основанных на моделях, которые коррелируют измеренные гемодинамические сигналы с контролируемыми экспериментальными переменными (Friston et al., 1994; Холмс и Фристон, 1998). В частности, каждый воксель изображения функциональной магнитно-резонансной томографии (фМРТ) и экспериментальная парадигма анализируются с помощью обобщенной линейной модели, и каждый воксель соответствует коэффициенту Bata уравнения регрессии, и все коэффициенты объединяются для формирования карты статистических параметров. (Yan et al., 2011; Wu et al., 2012). При групповом анализе для определения области активации группы выполняется тест t для одного образца на картах статистических параметров всех субъектов (Beckmann et al., 2003). Хотя GLM в настоящее время является доминирующим подходом к обнаружению активации мозга, растет интерес к многомерным подходам (Zhang et al., 2009). Например, машинное обучение как технология, управляемая данными, не только чувствительно к тонким шаблонам пространственной дифференциации, но также способно исследовать неотъемлемую многомерную природу данных изображений высокой размерности (Norman et al., 2006). Поскольку машинное обучение может находить функции, которые больше всего способствуют классификации (Meier et al., 2012; Lv et al., 2015), обнаруженные различия могут дать новое понимание физиологических механизмов областей мозга при различных задачах.
(Yan et al., 2011; Wu et al., 2012). При групповом анализе для определения области активации группы выполняется тест t для одного образца на картах статистических параметров всех субъектов (Beckmann et al., 2003). Хотя GLM в настоящее время является доминирующим подходом к обнаружению активации мозга, растет интерес к многомерным подходам (Zhang et al., 2009). Например, машинное обучение как технология, управляемая данными, не только чувствительно к тонким шаблонам пространственной дифференциации, но также способно исследовать неотъемлемую многомерную природу данных изображений высокой размерности (Norman et al., 2006). Поскольку машинное обучение может находить функции, которые больше всего способствуют классификации (Meier et al., 2012; Lv et al., 2015), обнаруженные различия могут дать новое понимание физиологических механизмов областей мозга при различных задачах.
Применение методов машинного обучения к данным нейровизуализации началось с работы Haxby et al. (2001), которые распознали характеристики распределения паттернов активации зрительной коры с помощью функциональной МРТ. В настоящее время машинное обучение широко используется в классификации данных фМРТ (Yan et al., 2017a, b) для изучения когнитивного состояния мозга (Yan et al., 2018). При разных условиях визуальной стимуляции стимулом могут быть разные визуальные картинки (предметы или люди, обувь или бутылки), растровая стимуляция под разными углами и т. Д., А тип задачи, получаемой субъектом, определяется путем классификации собранных данных фМРТ ( Haxby et al., 2001; Kamitani, Tong, 2005; Norman et al., 2006). Машинное обучение используется в психиатрии, чтобы отличать пациентов от контрольной. Пациенты с тяжелой депрессией (Fu et al., 2008) классифицировались с точностью от 70 до 80%.Лица и контрольная группа с расстройством аутистического спектра были выделены на основе двух экспериментов с фМРТ (Chanel et al., 2016). Таким образом, машинное обучение является многообещающим методом, используемым для определения состояния мозга (Ecker and Murphy, 2014). Машинное обучение в основном использует вспомогательные векторные машины в качестве классификаторов при классификации данных функционального магнитного резонанса (De et al.
В настоящее время машинное обучение широко используется в классификации данных фМРТ (Yan et al., 2017a, b) для изучения когнитивного состояния мозга (Yan et al., 2018). При разных условиях визуальной стимуляции стимулом могут быть разные визуальные картинки (предметы или люди, обувь или бутылки), растровая стимуляция под разными углами и т. Д., А тип задачи, получаемой субъектом, определяется путем классификации собранных данных фМРТ ( Haxby et al., 2001; Kamitani, Tong, 2005; Norman et al., 2006). Машинное обучение используется в психиатрии, чтобы отличать пациентов от контрольной. Пациенты с тяжелой депрессией (Fu et al., 2008) классифицировались с точностью от 70 до 80%.Лица и контрольная группа с расстройством аутистического спектра были выделены на основе двух экспериментов с фМРТ (Chanel et al., 2016). Таким образом, машинное обучение является многообещающим методом, используемым для определения состояния мозга (Ecker and Murphy, 2014). Машинное обучение в основном использует вспомогательные векторные машины в качестве классификаторов при классификации данных функционального магнитного резонанса (De et al. , 2008; Pereira et al., 2009; Ecker et al., 2010; Xin et al., 2013).
, 2008; Pereira et al., 2009; Ecker et al., 2010; Xin et al., 2013).
Когда количество функций намного превышает количество предметов, это вызовет проблему, которая обычно возникает в машинном обучении, известную как проклятие размерности (Bellman, 1961).Если уменьшение размеров элементов не может быть выполнено, это легко вызвать чрезмерную подгонку (Guyon, 2003). Чрезмерная подгонка означает, что модель имеет плохую способность к обобщению, то есть способность точно предсказать новые выборки плохая (Mayer et al., 2009). Следовательно, перед обучением модели требуется отбор признаков (De et al., 2007; Pereira et al., 2009; Mwangi et al., 2014).
В этом исследовании мы стремились изучить влияние активированных областей мозга и инактивированных областей мозга на результаты классификации данных функционального магнитного резонанса для различных задач.Мы извлекли среднее значение t обобщенной линейной модели в качестве собственного вектора и выбрали алгоритм регрессии Лассо (Tibshirani, 1996) для уменьшения размерности признаков. Используя линейную машину опорных векторов, классификационный вес использовался в качестве индекса для оценки важности каждой области мозга в классификации и сравнивался с результатами группового анализа. Результаты выявили две области мозга, которые не появлялись в активированной области мозга, но значительно повлияли на классификацию, а именно правая парацентральная долька и правая роландическая покрышка.
Используя линейную машину опорных векторов, классификационный вес использовался в качестве индекса для оценки важности каждой области мозга в классификации и сравнивался с результатами группового анализа. Результаты выявили две области мозга, которые не появлялись в активированной области мозга, но значительно повлияли на классификацию, а именно правая парацентральная долька и правая роландическая покрышка.
Материалы и методы
Участники
Экспериментальные данные для 1046 здоровых субъектов были получены из базы данных с открытым исходным кодом, WU-Minn Human Connectome Project (HCP) Data — 1200 Subjects (HCP_1200), опубликованной Public Connectome Data. Большинство участников были в возрасте от 22 до 35 лет. Все участники не имели ранее задокументированных историй психиатрических, неврологических или медицинских расстройств, влияющих на функцию их мозга. Из 1046 участников 560 были женщинами и 486 мужчинами, 223 — в возрасте от 22 до 25 лет, 455 — в возрасте от 26 до 30 лет, 357 — в возрасте от 31 до 35 лет и 11 — в возрасте старше 36 лет. .Мы использовали предварительно обработанные сеансы фМРТ 3T MR Language Task.
.Мы использовали предварительно обработанные сеансы фМРТ 3T MR Language Task.
Экспериментальные парадигмы
Языковое задание состояло из слухового рассказа с вопросами на понимание и математическими задачами. Он состоял из двух прогонов, каждый из которых состоял из восьми блоков (четыре сюжетных блока и четыре математических блока), случайно скомбинированных. Длина каждого блока варьировалась, но средняя длина составляла около 30 с. Чтобы выполнить 3,8-минутный пробег, блоки математических задач должны были соответствовать длине блоков сюжетных задач, а дополнительные математические задачи были добавлены, когда общая длина была меньше 3.8 мин. Сюжетные блоки представляли участникам краткую слуховую историю (около 5–9 предложений), адаптированную из сборника басен Эзопа. После каждого рассказа участнику задавали вопрос о теме рассказа в форме 2-альтернативного вопроса с принудительным выбором. Например, после рассказа об орле, спасающем человека, оказавшего ему услугу, участников спросили: «Это было из-за мести или взаимности?» Участники нажимали кнопку под указательным пальцем правой руки, чтобы выбрать первый вариант, или кнопку под средним пальцем правой руки, чтобы выбрать второй вариант.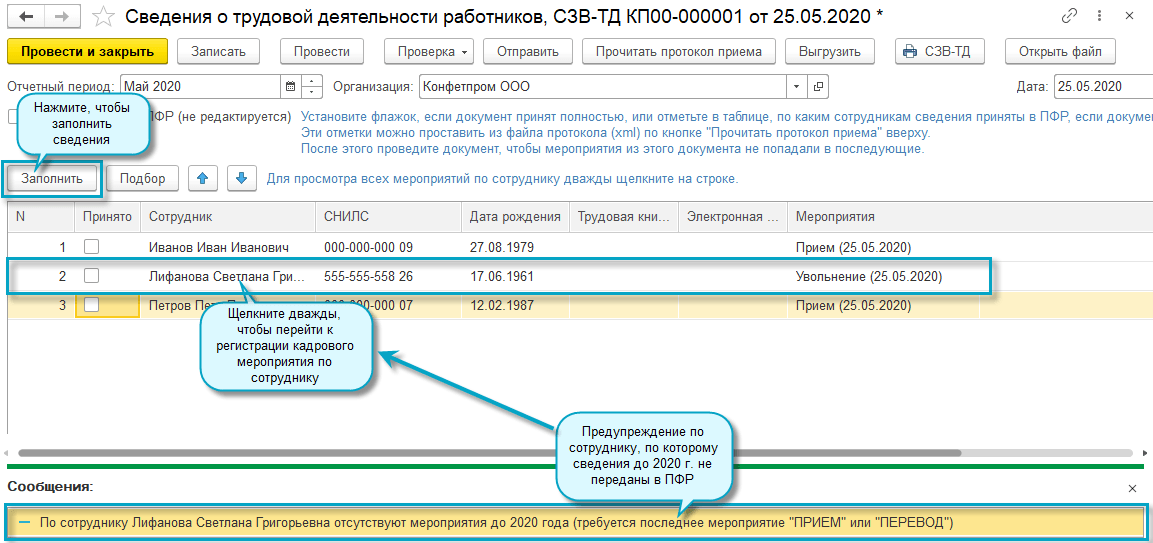 Математические задачи также были представлены в фонетической манере, требуя от участников выполнения простых задач на сложение и вычитание. Каждая серия арифметических операций оканчивалась словом «равно», за которым следовали два альтернативных варианта, например, «Четыре плюс двенадцать, минус два плюс девять, равно двадцать два или двадцать три?» Участники нажимали кнопку, чтобы выбрать первый или второй ответ (Binder et al., 2011; Barch et al., 2013).
Математические задачи также были представлены в фонетической манере, требуя от участников выполнения простых задач на сложение и вычитание. Каждая серия арифметических операций оканчивалась словом «равно», за которым следовали два альтернативных варианта, например, «Четыре плюс двенадцать, минус два плюс девять, равно двадцать два или двадцать три?» Участники нажимали кнопку, чтобы выбрать первый или второй ответ (Binder et al., 2011; Barch et al., 2013).
Сбор данных фМРТ
ЭПИ всего мозга были получены с помощью 32-канальной головной катушки на модифицированной 3T Siemens Skyra с TR = 720 мс, TE = 33.10 мс, угол поворота = 52 °, полоса пропускания = 2290 Гц / пик, поле зрения в плоскости = 208 × 180 мм, 72 среза, изотропные вокселы 2,0 мм, с многополосным коэффициентом ускорения 8 (Feinberg et al., 2010 ; Moeller et al., 2010). Для получения дополнительной информации, пожалуйста, обратитесь к Ugurbil et al. (2013) для обзора деталей приобретения задачи fMRI. Были получены два прогона каждой задачи, один с фазовым кодированием справа налево, а другой — с фазовым кодированием слева направо.
Обработка данных фМРТ
Предварительная обработка
Мы использовали предварительно обработанные данные fMRI 3T MR Language Task.Эти данные были обработаны с использованием FSL и FreeSurfer. Эти шаги включали устранение искажений градиента, коррекцию движения, коррекцию искажений EPI на основе карты поля, регистрацию EPI на основе границ мозга для структурного T1-взвешенного сканирования, нелинейную (FNIRT) регистрацию в пространстве MNI152 и нормализацию средней интенсивности. Кроме того, было выполнено пространственное сглаживание с гауссовой сердцевиной полной ширины 8 мм на полувысоте (рис. 1) для анализа GLM.
Рисунок 1. Блок-схема обработки данных для анализа SPM и машинного обучения.
Статистический анализ SPM
Чтобы выявить различия между двумя задачами и оценить значимость функциональной активации, мы использовали GLM-анализ. На первом уровне (внутрипредметного) анализа данные были умело смоделированы в GLM.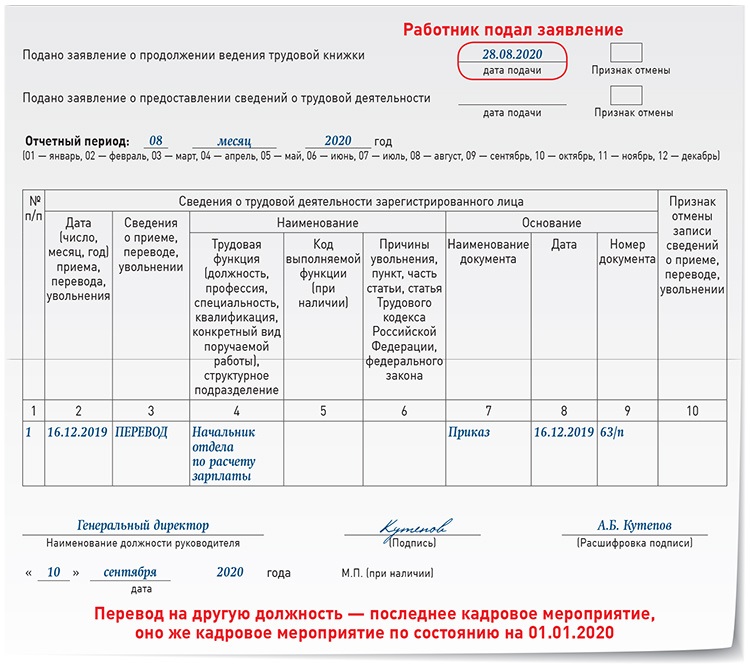 Для каждого участника были созданы четыре вида контрастных изображений, включая математическое задание, задание на сюжет, задание на математическое сравнение и задание на рассказ и математику. При анализе второго уровня использовались контрастные (con files) изображения из анализа первого уровня всех 1046 субъектов.Четыре условия были проанализированы с помощью анализа t для одной пробы. Была получена карта SPM (T) математических и сюжетных задач, и порог составил p <0,05 (FWE) на уровне вокселей. Чтобы устранить артефакты, мы использовали математические контрасты и контрасты историй в качестве маски, и порог маски составлял p <0,001 на уровне вокселей для задач математика против истории и история против математики, соответственно. Затем была получена карта SPM (T) математических и сюжетных задач и сюжетных и математических задач, и порог составил p <0.05 (FWE) на уровне вокселей. Эти результаты использовались для анализа активации функций мозга и сравнивались с результатами машинного обучения.
Для каждого участника были созданы четыре вида контрастных изображений, включая математическое задание, задание на сюжет, задание на математическое сравнение и задание на рассказ и математику. При анализе второго уровня использовались контрастные (con files) изображения из анализа первого уровня всех 1046 субъектов.Четыре условия были проанализированы с помощью анализа t для одной пробы. Была получена карта SPM (T) математических и сюжетных задач, и порог составил p <0,05 (FWE) на уровне вокселей. Чтобы устранить артефакты, мы использовали математические контрасты и контрасты историй в качестве маски, и порог маски составлял p <0,001 на уровне вокселей для задач математика против истории и история против математики, соответственно. Затем была получена карта SPM (T) математических и сюжетных задач и сюжетных и математических задач, и порог составил p <0.05 (FWE) на уровне вокселей. Эти результаты использовались для анализа активации функций мозга и сравнивались с результатами машинного обучения.
Классификация с использованием машинного обучения
После того, как SPM обработал отдельные данные, файл spmT был создан для каждого из двух экспериментальных условий. В рамках GRETNA (Wang et al., 2015) шаблон AAL90 (Anatomical Automatic Labeling) использовался для сегментации области мозга из файла spmT, и было извлечено среднее статистическое значение T для каждой области мозга, чтобы сгенерировать 90 × 1 матрица характеристик.Для 1046 участников вектор признаков был следующим: математическое задание 1046 × 90, сюжетное задание 1046 × 90. В качестве обучающей выборки были выбраны характеристики 800 субъектов. Тег математической задачи был равен 1, тег задачи истории был равен -1, а обучающий набор был отправлен классификатору для классификации. Остальные 246 испытуемых использовались в качестве набора тестов для предсказания. Перед классификацией для нормализации предварительно обработанного обучающего набора использовалась z-оценка. А для выбора признаков использовался алгоритм регрессии Лассо. Затем машина линейных опорных векторов использовалась в качестве функции ядра, и 10-кратная перекрестная проверка использовалась для расчета правильной скорости обучения. Результаты вклада области мозга также могут быть получены при создании модели классификации. Наконец, набор тестов был отправлен классификатору для получения классификационной метки, и была рассчитана точность результата прогноза. Чтобы получить оптимальный результат классификации, необходимо было отладить параметры классификации, чтобы предсказать правильность результатов в качестве стандарта отладки.Он включал два параметра, один из которых был параметром регуляризации α алгоритма Лассо, и он напрямую определял количество функций. Чем больше альфа, тем реже модель, поэтому для большего числа коэффициентов регрессии β было установлено значение 0, таким образом удаляя некоторые функции для достижения выбора функций. Другое был коэффициент штрафа C линейных опорных векторов, и она непосредственно определяется точностью обучения.
Затем машина линейных опорных векторов использовалась в качестве функции ядра, и 10-кратная перекрестная проверка использовалась для расчета правильной скорости обучения. Результаты вклада области мозга также могут быть получены при создании модели классификации. Наконец, набор тестов был отправлен классификатору для получения классификационной метки, и была рассчитана точность результата прогноза. Чтобы получить оптимальный результат классификации, необходимо было отладить параметры классификации, чтобы предсказать правильность результатов в качестве стандарта отладки.Он включал два параметра, один из которых был параметром регуляризации α алгоритма Лассо, и он напрямую определял количество функций. Чем больше альфа, тем реже модель, поэтому для большего числа коэффициентов регрессии β было установлено значение 0, таким образом удаляя некоторые функции для достижения выбора функций. Другое был коэффициент штрафа C линейных опорных векторов, и она непосредственно определяется точностью обучения. Значение C обычно составляло от 0,01 до 0,1. Вклад области мозга был предложен при двух предварительных условиях: во-первых, признак был извлечен на основе области, разделенной шаблоном мозга, так что признак был связан с трехмерной структурой мозга, следовательно, каждый признак соответствовал мозгу. область, край; во-вторых, машина линейных опорных векторов была выбрана в качестве классификатора, потому что вес линейной машины опорных векторов находился во взаимно однозначном соответствии с вектором признаков.Чем больше значение веса, тем важнее была соответствующая характеристика для определения поверхности принятия решения о классификации. Благодаря взаимосвязи между характеристиками и областями мозга, а также взаимосвязью между характеристиками и классификационными весами была установлена соответствующая взаимосвязь между областями мозга и весами. Проще говоря, вклад области мозга был значением веса функции оптимального решения линейного машинного классификатора опорных векторов.
Значение C обычно составляло от 0,01 до 0,1. Вклад области мозга был предложен при двух предварительных условиях: во-первых, признак был извлечен на основе области, разделенной шаблоном мозга, так что признак был связан с трехмерной структурой мозга, следовательно, каждый признак соответствовал мозгу. область, край; во-вторых, машина линейных опорных векторов была выбрана в качестве классификатора, потому что вес линейной машины опорных векторов находился во взаимно однозначном соответствии с вектором признаков.Чем больше значение веса, тем важнее была соответствующая характеристика для определения поверхности принятия решения о классификации. Благодаря взаимосвязи между характеристиками и областями мозга, а также взаимосвязью между характеристиками и классификационными весами была установлена соответствующая взаимосвязь между областями мозга и весами. Проще говоря, вклад области мозга был значением веса функции оптимального решения линейного машинного классификатора опорных векторов.
Результаты
Поведенческие данные
Поведенческие данные были собраны у 1046 участников во время экспериментов с фМРТ. В ходе эксперимента были потеряны данные только об одном испытуемом. Мы использовали среднее время реакции и правильные данные 1045 участников для статистического анализа. Было две задачи. Среднее время реакции (RT) (Рисунок 2A) и средняя точность (Рисунок 2B) составили 3,79 ± 0,38 с и 83,28% (SD 3,42), соответственно, для математической задачи и 3,50 ± 0,39 с и 92.57% (СО 12,94) соответственно для сюжетного задания. Двухсторонние двухвыборочные тесты t были выполнены для сравнения средних значений RT и средней точности между математической задачей и сюжетной задачей. Результаты показали, что математическое задание имело более медленное время реакции по сравнению с заданием на рассказ ( t = 17,260, P <0,001). А точность математического задания была значительно ниже, чем у задания-рассказа ( t = 15.834, P <0. 001).
001).
Рисунок 2. Поведенческие результаты. (A) Среднее время реакции на математические и сюжетные стимулы. (B) Средние показатели точности математических и сюжетных стимулов.
Данные изображений
Результаты группового анализа
Конкретные групповые результаты для четырех групп активированных областей мозга были показаны в таблице 1. Активация математических и сюжетных задач показала, что активировались левая и правая височные доли (рисунки 3A, B). В дополнение к височной доле в математической задаче область мозга с большей интенсивностью активации включала: левый прецентральный гирус, левый средний височный гирус, левый верхний височный гирус, правый нижний лобный гирус и правый средний фронтальный гирус (Wang et al. al., 2007). В сюжетном задании области мозга с большей интенсивностью активации включали: левую нижнюю лобную гирю, левую среднюю лобную гирю и правую нижнюю полулунную дольку. По сравнению с результатами рассказа (рис. 3C) математические результаты включали: левую нижнюю лобную дольку, левую нижнюю теменную дольку и левую верхнюю теменную дольку, которые имели более высокую интенсивность активации, чем сюжетная задача; в то время как верхняя теменная долька и нижняя теменная долька активируются только в математической задаче.По сравнению с результатами математики (рис. 3D), область мозга в сюжетной задаче, левая нижняя височная спираль, верхняя височная спираль и средняя височная спираль имели значительно более высокую интенсивность активации, чем математическая задача, и парагиппокампальная мышца миндалины на левая и правая стороны активируются только в сюжетной задаче (Binder et al., 2011; Barch et al., 2013).
3C) математические результаты включали: левую нижнюю лобную дольку, левую нижнюю теменную дольку и левую верхнюю теменную дольку, которые имели более высокую интенсивность активации, чем сюжетная задача; в то время как верхняя теменная долька и нижняя теменная долька активируются только в математической задаче.По сравнению с результатами математики (рис. 3D), область мозга в сюжетной задаче, левая нижняя височная спираль, верхняя височная спираль и средняя височная спираль имели значительно более высокую интенсивность активации, чем математическая задача, и парагиппокампальная мышца миндалины на левая и правая стороны активируются только в сюжетной задаче (Binder et al., 2011; Barch et al., 2013).
Таблица 1. Активированные области во время двух слуховых стимулов и различные активированные области между ними.
Рисунок 3. Глобальная активация мозга группового анализа. (A) Math показывает трехмерную карту активации мозга в математической задаче.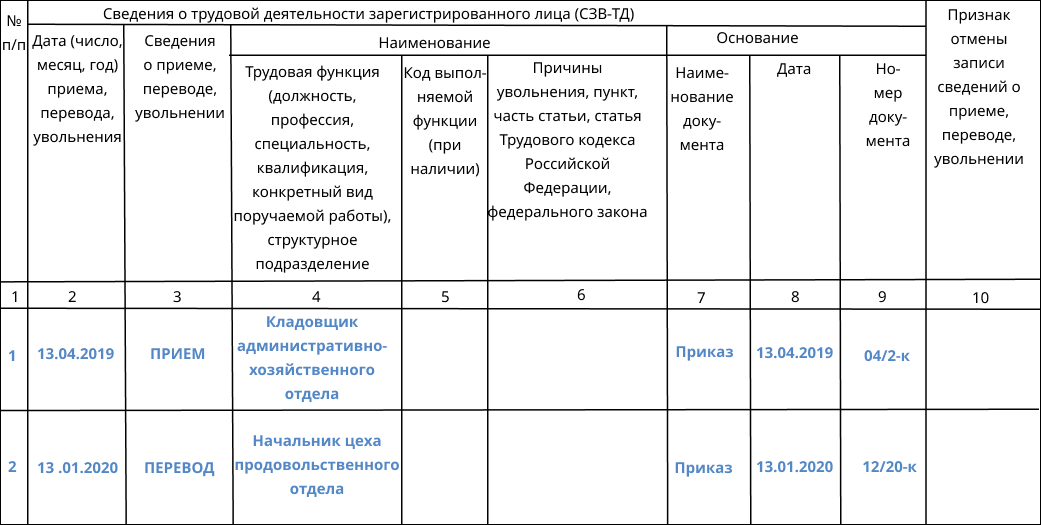 (B) Рассказ показывает трехмерную карту активации мозга в сюжетном задании. (C) Математика против рассказа показывает разницу активированных областей мозга между математической задачей и историей. (D) Story vs. Math показывает разницу активированных областей мозга между заданием Story и заданием Math.WM = рабочая память, IPS = внутри теменная борозда, AC = слуховая кора, SMA = дополнительная моторная область.
(B) Рассказ показывает трехмерную карту активации мозга в сюжетном задании. (C) Математика против рассказа показывает разницу активированных областей мозга между математической задачей и историей. (D) Story vs. Math показывает разницу активированных областей мозга между заданием Story и заданием Math.WM = рабочая память, IPS = внутри теменная борозда, AC = слуховая кора, SMA = дополнительная моторная область.
Результат отладки параметра
Как показано на рисунке 4A, было обнаружено, что по мере увеличения α количество функций уменьшается экспоненциально. Следовательно, чтобы уменьшить размерную катастрофу и улучшить характеристики классификации классификатора, было выбрано соответствующее количество важных характеристик, α было принято равным: 0,001, 0,002, 0,003, 0,005, 0,007, 0.01, и соответствующие номера функций были: 38, 25, 19, 11, 9, 8. Далее, коэффициент штрафа С линейного опорных векторов была отлажена, и, наконец, точность результата прогнозирования был использован в качестве критерия для оценка работы классификатора. Как показано на рисунке 4B, когда α = 0,002, C = 0,09, наивысшая степень точности классификации составила 87,60%. Текущие параметры и эффекты обученных моделей можно было визуально оценить, построив кривую ROC и индикатор AUC.Как показано на рисунке 4C, площадь под кривой составила 0,96, что близко к 1, что указывает на хороший эффект классификации.
Как показано на рисунке 4B, когда α = 0,002, C = 0,09, наивысшая степень точности классификации составила 87,60%. Текущие параметры и эффекты обученных моделей можно было визуально оценить, построив кривую ROC и индикатор AUC.Как показано на рисунке 4C, площадь под кривой составила 0,96, что близко к 1, что указывает на хороший эффект классификации.
Рисунок 4. (A) Взаимосвязь между параметром регуляризации альфа алгоритма регрессии Лассо и количеством выбранных признаков (B) Взаимосвязь между штрафным коэффициентом C линейной машины векторов поддержки и правильным скорость результата прогноза при различных значениях альфа (C) Кривая ROC оптимальных результатов классификации.
Результаты машинного обучения
Как показано на рисунке 5, была показана трехмерная карта распределения вклада областей мозга в шести направлениях. Некоторые регионы имели более высокий классификационный вес, чем другие. В частности, если вес некоторых областей был, по крайней мере, больше, чем средний вес всех областей, плюс стандартное отклонение в один раз, мы считали эти области значимыми (Tian et al. , 2011). Среднее значение плюс стандартное отклонение вклада было равно 0.0614. Участок мозга с вкладом более 0,0614 считался значимым, в том числе: правая парацентральная долька, правая Rolandic Operculum и правая нижняя теменная долька, за исключением надмаргинальной и угловой извилин.
, 2011). Среднее значение плюс стандартное отклонение вклада было равно 0.0614. Участок мозга с вкладом более 0,0614 считался значимым, в том числе: правая парацентральная долька, правая Rolandic Operculum и правая нижняя теменная долька, за исключением надмаргинальной и угловой извилин.
Рис. 5. Трехмерный вклад областей мозга в классификацию. Каждый узел представлял область мозга, разделенную на AAL90 (шаблон анатомической автоматической маркировки). Цвета узлов представляют разные области, а размер узла масштабируется в соответствии со значением веса областей мозга.Чем больше вклад области мозга, тем больше радиус узла.
Сравнивая результаты классифицированного вклада области мозга и результаты области активации группового анализа, как показано в таблице 2, было обнаружено, что 13 из 25 характерных областей мозга перекрываются с активированными областями мозга группового анализа. Среди 13 областей мозга было 11 областей мозга, которые перекрывались с другой картой активации между математическим заданием и заданием-рассказом.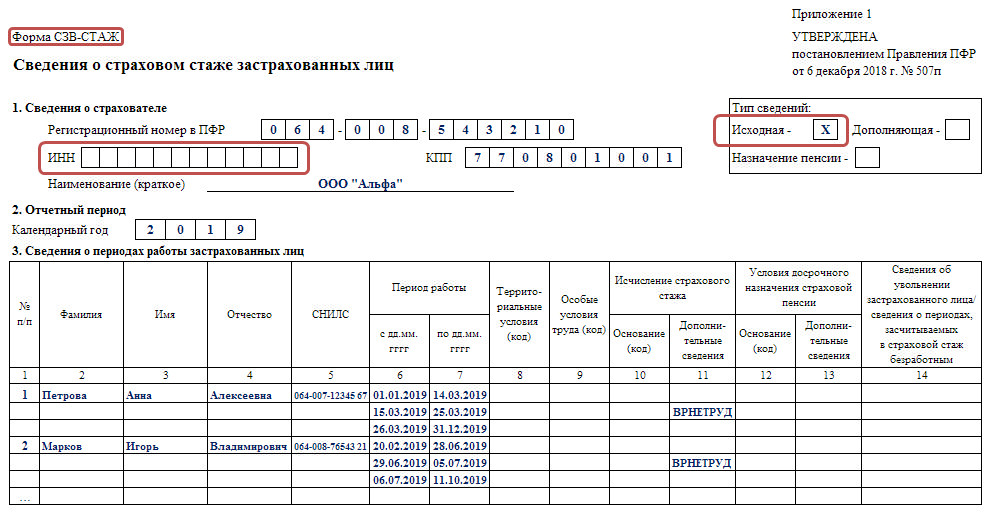 К 11 областям мозга относились: левая и правая нижняя теменная доля (не включая супрамаргинальные и угловые извилины), левая и правая средняя лобная мозоль, левая супрамаргинальная мозоль, правая верхняя париетальная мозоль, правая верхняя лобная мозоль, дорсолатеральная, правая нижняя лобная мозоль, Оперкулярная часть, правая Angular Gyrus, левая Amygdala, левая Heschl Gyrus.Более того, эти совпадающие регионы сильно активизировались в результатах группового анализа (значения t были больше 18). Остальные 12 областей мозга не совпадали с результатами областей активации группового анализа, включая две области мозга, которые внесли значительный вклад: правая парацентральная долька и правая роландическая покрышка.
К 11 областям мозга относились: левая и правая нижняя теменная доля (не включая супрамаргинальные и угловые извилины), левая и правая средняя лобная мозоль, левая супрамаргинальная мозоль, правая верхняя париетальная мозоль, правая верхняя лобная мозоль, дорсолатеральная, правая нижняя лобная мозоль, Оперкулярная часть, правая Angular Gyrus, левая Amygdala, левая Heschl Gyrus.Более того, эти совпадающие регионы сильно активизировались в результатах группового анализа (значения t были больше 18). Остальные 12 областей мозга не совпадали с результатами областей активации группового анализа, включая две области мозга, которые внесли значительный вклад: правая парацентральная долька и правая роландическая покрышка.
Таблица 2. Сравнение со степенями между вкладом области мозга и групповым анализом: Метка и области представляют метку области мозга и название области мозга результата классификации по шаблону AAL90.
Обсуждение
Одна из экспериментальных парадигм, разработанная Wang et al.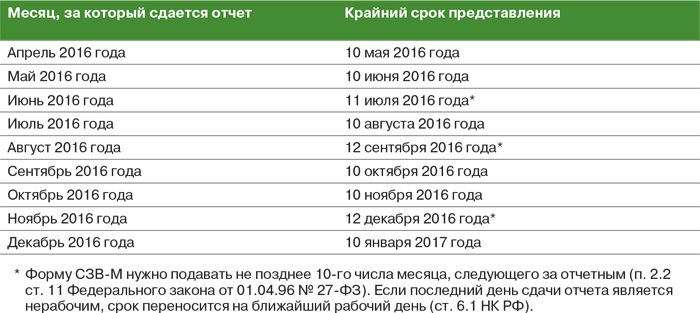 была задача слуховых вычислений на китайском и английском языках. Расчет включал сложение и умножение. Это похоже на математическое задание. В исследовании приняли участие 19 взрослых носителей китайского языка, у которых не было нарушений речи или слуха. Активные области мозга для выполнения вычислительной задачи на английском языке после группового анализа включают в себя: левую прецентральную гирю, левую среднюю височную гирю, правую нижнюю лобную гирю и правую среднюю лобную гирю (Wang et al., 2007). Barch et al. (2013) выбрали 77 участников (58 женщин и 19 мужчин), все участники были в возрасте от 22 до 35 лет, без ранее задокументированных историй психиатрических, неврологических или медицинских расстройств, которые, как известно, влияют на функцию мозга. Binder et al. (2011) выбрали 34 здоровых взрослых правши в качестве участников. (17 женщин и 17 мужчин) в возрасте от 18 до 50 лет (в среднем 29 лет). Все они использовали ту же экспериментальную парадигму, что и в этой статье, и были получены аналогичные результаты: история vs.
была задача слуховых вычислений на китайском и английском языках. Расчет включал сложение и умножение. Это похоже на математическое задание. В исследовании приняли участие 19 взрослых носителей китайского языка, у которых не было нарушений речи или слуха. Активные области мозга для выполнения вычислительной задачи на английском языке после группового анализа включают в себя: левую прецентральную гирю, левую среднюю височную гирю, правую нижнюю лобную гирю и правую среднюю лобную гирю (Wang et al., 2007). Barch et al. (2013) выбрали 77 участников (58 женщин и 19 мужчин), все участники были в возрасте от 22 до 35 лет, без ранее задокументированных историй психиатрических, неврологических или медицинских расстройств, которые, как известно, влияют на функцию мозга. Binder et al. (2011) выбрали 34 здоровых взрослых правши в качестве участников. (17 женщин и 17 мужчин) в возрасте от 18 до 50 лет (в среднем 29 лет). Все они использовали ту же экспериментальную парадигму, что и в этой статье, и были получены аналогичные результаты: история vs. Результаты математики показали, что наибольший кластер активации затрагивает височную долю, а сильная медиальная временная активация — ункус, миндалевидное тело и передний гиппокамп, переходя кзади в парагиппокамп и заднюю веретенообразную извилину.
Результаты математики показали, что наибольший кластер активации затрагивает височную долю, а сильная медиальная временная активация — ункус, миндалевидное тело и передний гиппокамп, переходя кзади в парагиппокамп и заднюю веретенообразную извилину.
Сравнительный анализ вклада областей мозга и результатов группы
Вклад областей мозга заключается в объединении различных разделов трехмерной физиологической структуры в пространстве мозга с весами классификаторов.Таким образом, степень вклада области мозга отражает важность различных областей мозга для результатов классификации. Чем выше значение вклада, тем важнее область мозга для результатов классификации. Классификация заключается в сравнении различий между двумя категориями. Таким образом, результаты классификации в основном совпадали с дифференциальной активацией области мозга. Этими перекрывающимися областями мозга были: Средняя лобная извилина, которая участвует в процессах выразительности языка, включая семантику (Brown et al. , 2010), грамматика и синтаксис. Область Брока играла роль в синтаксической обработке во время понимания прочитанного на китайском, беглости речи (Abrahams et al., 2003) и вербальной рабочей памяти (Leung et al., 2002). Нижняя теменная долька участвует в восприятии эмоций, лицевых стимулов и интерпретации сенсорной информации. Левая супрамаргинальная Gyrus, скорее всего, была связана с восприятием и обработкой языка (Gazzaniga et al., 2013). Левый Heschl Gyrus, который находится в области первичной слуховой коры, погребенной в боковой борозде человеческого мозга, был первой корковой структурой, обрабатывающей поступающую слуховую информацию.Heschl Gyrus был активен во время обработки слуха с помощью фМРТ для тональных и семантических задач (Warrier et al., 2009). Правая верхняя лобная масса, дорсолатеральная, участвует в самосознании в координации с действием сенсорной системы (Goldberg and Harel, 2006; Wang et al., 2017). Миндалевидное тело играет важную роль в памяти, принятии решений и эмоциональной реакции (включая страх, тревогу и агрессию), которая считается частью лимбической системы (Amunts et al.
, 2010), грамматика и синтаксис. Область Брока играла роль в синтаксической обработке во время понимания прочитанного на китайском, беглости речи (Abrahams et al., 2003) и вербальной рабочей памяти (Leung et al., 2002). Нижняя теменная долька участвует в восприятии эмоций, лицевых стимулов и интерпретации сенсорной информации. Левая супрамаргинальная Gyrus, скорее всего, была связана с восприятием и обработкой языка (Gazzaniga et al., 2013). Левый Heschl Gyrus, который находится в области первичной слуховой коры, погребенной в боковой борозде человеческого мозга, был первой корковой структурой, обрабатывающей поступающую слуховую информацию.Heschl Gyrus был активен во время обработки слуха с помощью фМРТ для тональных и семантических задач (Warrier et al., 2009). Правая верхняя лобная масса, дорсолатеральная, участвует в самосознании в координации с действием сенсорной системы (Goldberg and Harel, 2006; Wang et al., 2017). Миндалевидное тело играет важную роль в памяти, принятии решений и эмоциональной реакции (включая страх, тревогу и агрессию), которая считается частью лимбической системы (Amunts et al.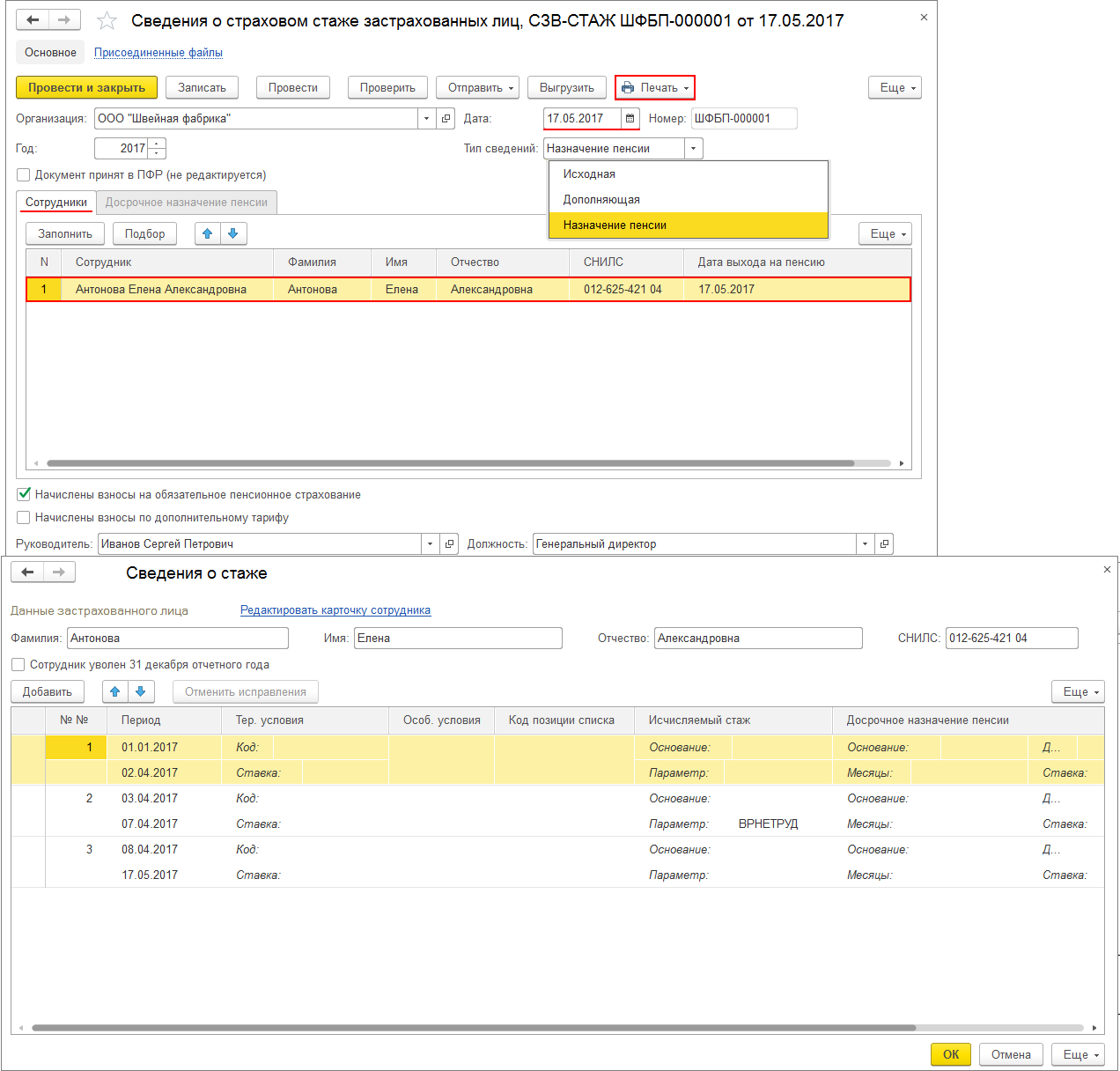 , 2005). Левая миндалина играет важную роль в памяти, принятии решений и эмоциональной реакции (включая страх, тревогу и агрессию), которая считается частью лимбической системы (Amunts et al., 2005). Более того, интенсивность активации этих перекрывающихся областей мозга в результатах группового анализа отражала правильность классификационных признаков и могла идентифицировать области мозга с большими различиями в активации между двумя задачами.
, 2005). Левая миндалина играет важную роль в памяти, принятии решений и эмоциональной реакции (включая страх, тревогу и агрессию), которая считается частью лимбической системы (Amunts et al., 2005). Более того, интенсивность активации этих перекрывающихся областей мозга в результатах группового анализа отражала правильность классификационных признаков и могла идентифицировать области мозга с большими различиями в активации между двумя задачами.
В особой области мозга было 12 областей мозга, которые не совпадали с результатами групповой активации, в том числе две области мозга со значительным вкладом: правая парацентральная долька, которая связана с моторной и сенсорной иннервацией контралатеральной нижней конечности (Spasojević et al. al., 2013), он также отвечает за контроль дефекации и мочеиспускания, а также за правильную Rolandic Operculum. Некоторые исследования доказали, что нарушения артикуляции соответствуют поражениям Rolandic Operculum (Tonkonogy and Goodglass, 1981). Причину значительной разницы между результатом классификации и результатом группового анализа можно объяснить на примере области мозга парацентральной дольки. С одной стороны, при сравнении областей мозга двух различий задач в групповом анализе маска (Gajdoš et al., 2016) был добавлен для исключения псевдоактивации. Маска определялась активацией области мозга математической или сюжетной задачи. Как показано на рисунке 6, значение T области мозга (метка номер 70) было отрицательным для обеих задач. Следовательно, дифференциальная активация области мозга должна быть включена в объем области мозга активации отдельной задачи. Основная функция области головного мозга парацентральной дольки — контролировать движение контралатеральных нижних конечностей и сенсорную иннервацию.Функциональность Парацентральной дольки не зависела от активации задачи и не активировалась при отдельном анализе математических и сюжетных задач. Следовательно, разные области мозга при выполнении этих двух задач вряд ли покажут активацию в области парацентральной дольки.
Причину значительной разницы между результатом классификации и результатом группового анализа можно объяснить на примере области мозга парацентральной дольки. С одной стороны, при сравнении областей мозга двух различий задач в групповом анализе маска (Gajdoš et al., 2016) был добавлен для исключения псевдоактивации. Маска определялась активацией области мозга математической или сюжетной задачи. Как показано на рисунке 6, значение T области мозга (метка номер 70) было отрицательным для обеих задач. Следовательно, дифференциальная активация области мозга должна быть включена в объем области мозга активации отдельной задачи. Основная функция области головного мозга парацентральной дольки — контролировать движение контралатеральных нижних конечностей и сенсорную иннервацию.Функциональность Парацентральной дольки не зависела от активации задачи и не активировалась при отдельном анализе математических и сюжетных задач. Следовательно, разные области мозга при выполнении этих двух задач вряд ли покажут активацию в области парацентральной дольки. С другой стороны, исходя из принципа классификации (Черкасский, 1997), машинное обучение не обязано рассматривать проблему псевдоактивации. Выбор функций ограничивался не диапазоном активации, а всем диапазоном мозга.Машина линейных опорных векторов отображала вектор признаков из пространства Евклида в гильбертово пространство, делая набор данных линейно разделяемым в многомерном пространстве. В гильбертовом пространстве нахождение такой поверхности принятия решений не только разделяло два типа функций, но также делало расстояние между двумя типами функций до этой поверхности принятия решения как можно большим (Schölkopf, 2000; Huang et al., 2012). Чем больше расстояние между двумя типами функций, тем больше вес классификатора и больше значение вклада области мозга, соответствующей этой функции.Таким образом, вклад по существу отражает разницу между двумя типами особенностей, соответствующих области мозга в гильбертовом пространстве. Область мозга парацентральной дольки имела наибольший вклад, что указывает на то, что расстояние между соответствующими функциями области мозга было очень большим в многомерном пространстве.
С другой стороны, исходя из принципа классификации (Черкасский, 1997), машинное обучение не обязано рассматривать проблему псевдоактивации. Выбор функций ограничивался не диапазоном активации, а всем диапазоном мозга.Машина линейных опорных векторов отображала вектор признаков из пространства Евклида в гильбертово пространство, делая набор данных линейно разделяемым в многомерном пространстве. В гильбертовом пространстве нахождение такой поверхности принятия решений не только разделяло два типа функций, но также делало расстояние между двумя типами функций до этой поверхности принятия решения как можно большим (Schölkopf, 2000; Huang et al., 2012). Чем больше расстояние между двумя типами функций, тем больше вес классификатора и больше значение вклада области мозга, соответствующей этой функции.Таким образом, вклад по существу отражает разницу между двумя типами особенностей, соответствующих области мозга в гильбертовом пространстве. Область мозга парацентральной дольки имела наибольший вклад, что указывает на то, что расстояние между соответствующими функциями области мозга было очень большим в многомерном пространстве. Мы предположили, что разница в этой области мозга не была очевидна в низкоразмерном пространстве, и статистический анализ не показал какой-либо значимости.
Мы предположили, что разница в этой области мозга не была очевидна в низкоразмерном пространстве, и статистический анализ не показал какой-либо значимости.
Рис. 6. Среднее значение T в инактивированных областях мозга при выполнении двух задач. Цифры на 12-столбцовой диаграмме представляют номер области мозга шаблона AAL90, серое поле представляет математическую задачу, а оранжевый — сюжетную задачу. Число звездочек представляет собой степень значения p . ∗ p <0,05, ∗∗ p <0,01, ∗∗∗ p <0.001.
Машинное обучение использовало разницу между двумя задачами для классификации. Среди отрицательно активированных областей мозга разница была более очевидной, поэтому вклад в классификацию был выше, чем вклад в активированной области мозга. Однако механизм этих отрицательно активированных областей мозга при выполнении задач остается неясным. Это связано с тем, что в двух задачах, используемых в задействованных областях мозга, механизм сильно отличался от механизма негативной активации области мозга, поэтому не было необходимости использовать области мозга с негативной активацией для выполнения задачи. В зависимости от снабжения мозговым кровотоком, чем выше степень корреляции регионарной функции, тем больше степень кровоснабжения головного мозга.
В зависимости от снабжения мозговым кровотоком, чем выше степень корреляции регионарной функции, тем больше степень кровоснабжения головного мозга.
Мы сравнили значения T 12 неактивных областей мозга для двух задач, как показано на рисунке 6. Значения T областей мозга в обеих задачах были в основном отрицательными, а парный образец t -тест в основном имел p значение менее 0,05. Это показало, что существует значительная разница между двумя задачами в отрицательной активации областей мозга.Отрицательная активация областей мозга сильно различалась для разных задач, предполагая, что помимо активации областей мозга, отрицательная активация областей мозга играла важную роль в исследованиях мозга.
Для изучения вклада области мозга в классификацию в качестве классификатора была выбрана машина линейных опорных векторов, поскольку значение веса классификатора отражало важность характеристики для классификатора. Кроме того, в качестве метода выбора признаков была выбрана регрессия Лассо, которая была связана с обучением окончательной модели алгоритма машинного обучения.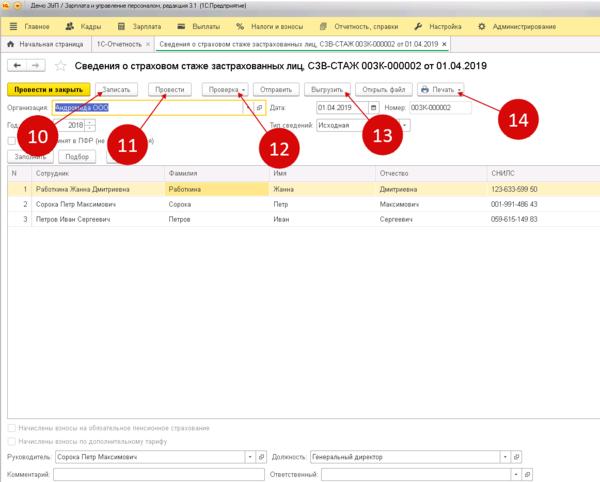 Обучающая модель была обучена на основе входных обучающих данных. После завершения обучения функции были отсортированы на основе представления модели и важности функций. Это был всего лишь отбор. Если функция имеет сильное влияние на эффективность классификации, она будет сохранена и будет равна нулю, если не влияет на классификатор. Этот метод не изменил соответствие между областями мозга и особенностями.
Обучающая модель была обучена на основе входных обучающих данных. После завершения обучения функции были отсортированы на основе представления модели и важности функций. Это был всего лишь отбор. Если функция имеет сильное влияние на эффективность классификации, она будет сохранена и будет равна нулю, если не влияет на классификатор. Этот метод не изменил соответствие между областями мозга и особенностями.
Заключение
В этой статье среднее значение T однократной обобщенной линейной модели было извлечено как собственный вектор.Для классификации использовались алгоритм регрессии Лассо и машина линейных опорных векторов, и результат сравнивался с результатом активации группового анализа SPM. Было обнаружено, что есть совпадающие области мозга и несовпадающие области мозга: совпадающие области мозга в основном были различием между задачами по активации областей мозга, и интенсивность активации была высокой. Несовпадающие области мозга включали области мозга со значительным классификационным вкладом, правая парацентральная долька и правая роландическая покрышка.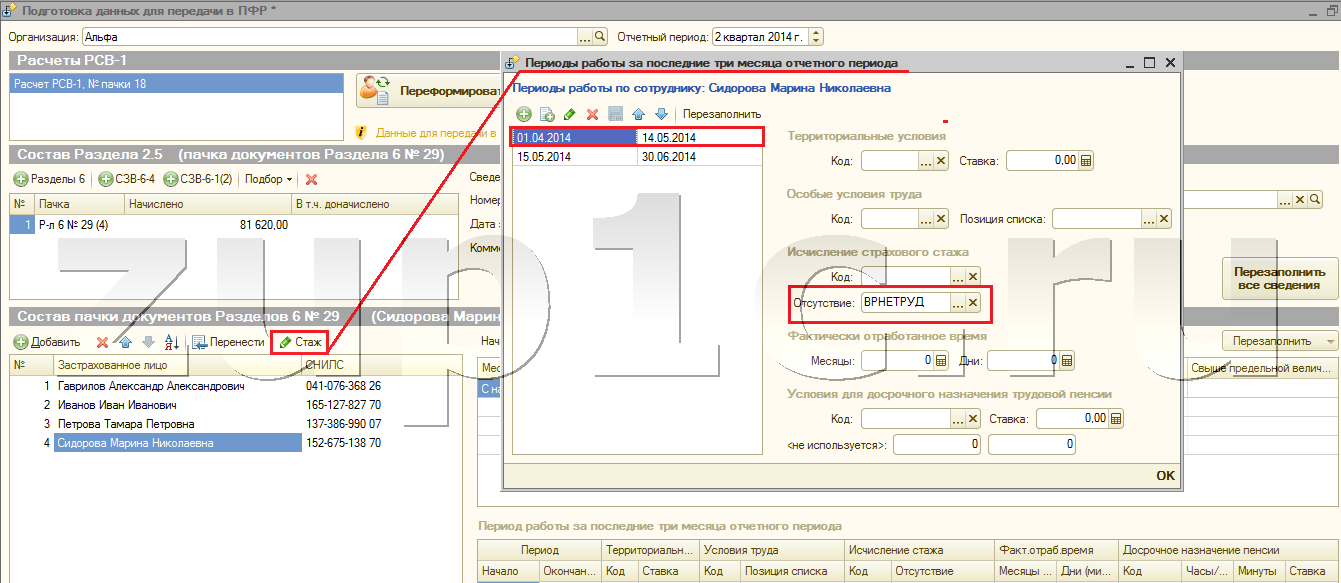 Разница между двумя результатами в основном связана с различием в алгоритме. В статистическом анализе, чтобы исключить псевдоактивацию, дифференциальная активация была ограничена диапазоном активации одной задачи; в то время как машинное обучение не нужно было рассматривать псевдоактивацию, которая может происходить из области всего мозга, оно обнаружило особенности областей мозга, которые не были связаны с активацией задачи, но значительно способствовали классификации. Таким образом, вклад области мозга был с другой точки зрения, анализируя разницу между двумя состояниями активности мозга и находя важные области мозга без статистической разницы.Это предполагает важную роль отрицательной активации областей мозга в исследованиях мозга.
Разница между двумя результатами в основном связана с различием в алгоритме. В статистическом анализе, чтобы исключить псевдоактивацию, дифференциальная активация была ограничена диапазоном активации одной задачи; в то время как машинное обучение не нужно было рассматривать псевдоактивацию, которая может происходить из области всего мозга, оно обнаружило особенности областей мозга, которые не были связаны с активацией задачи, но значительно способствовали классификации. Таким образом, вклад области мозга был с другой точки зрения, анализируя разницу между двумя состояниями активности мозга и находя важные области мозга без статистической разницы.Это предполагает важную роль отрицательной активации областей мозга в исследованиях мозга.
Доступность данных
В данном исследовании были проанализированы общедоступные наборы данных. Эти данные можно найти здесь: https://db.humanconnectome.org/.
Авторские взносы
MW, CL, JW, YL, XZ и XL проанализировали данные с помощью SPM.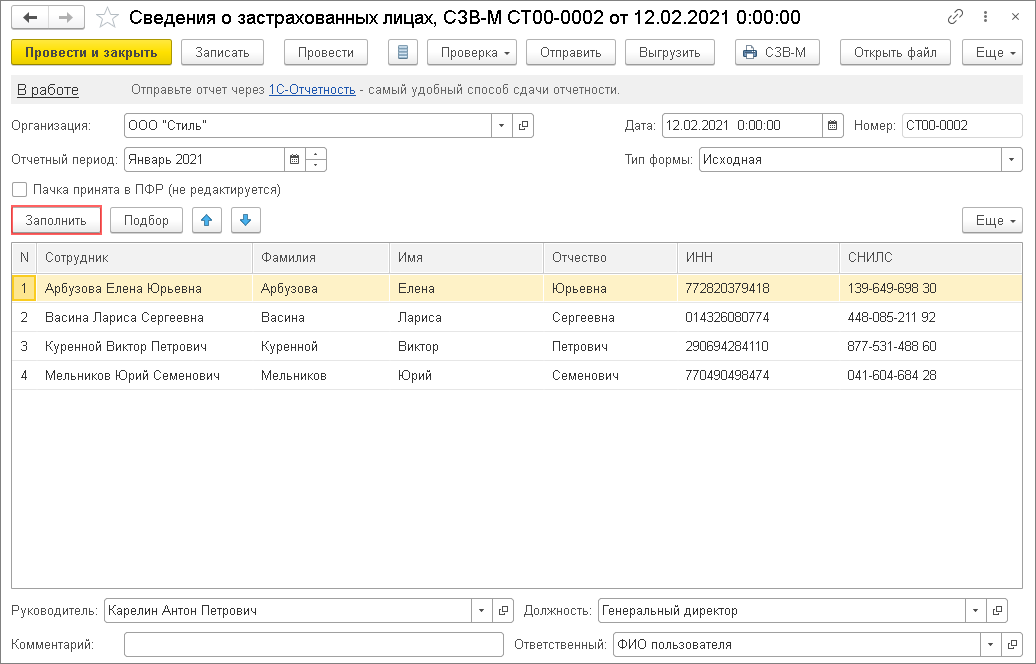 MW, WZ, RC, YW и YF проанализировали данные с помощью машинного обучения. MW и CL подготовили рисунки и составили рукопись. WZ и RC внесли значительный вклад в написание и редактирование рукописи.Все авторы внесли свой вклад в разработку рукописи, а также прочитали и одобрили окончательную рукопись.
MW, WZ, RC, YW и YF проанализировали данные с помощью машинного обучения. MW и CL подготовили рисунки и составили рукопись. WZ и RC внесли значительный вклад в написание и редактирование рукописи.Все авторы внесли свой вклад в разработку рукописи, а также прочитали и одобрили окончательную рукопись.
Финансирование
Это исследование финансировалось за счет грантов Национального фонда естественных наук Китая (гранты №№ 61727807, 81771909, 31600933, 61701323, 81671776 и 61633018), Пекинской городской комиссии по науке и технологиям (гранты № Z161100002616020, Z131100006813022). и PXM2017_026283_000002), План Ян Фань Муниципального управления больниц Пекина (клинический инновационный проект, грант No.XMLX201714), Фундаментальные и клинические фонды Столичного медицинского университета Китая (гранты № 16JL-L08 и 17JL68) и Пекинская программа выдающихся талантов (грант № 2016000020124G098).
Заявление о конфликте интересов
Авторы заявляют, что исследование проводилось в отсутствие каких-либо коммерческих или финансовых отношений, которые могут быть истолкованы как потенциальный конфликт интересов.
Сноски
- https: //db.humanconnectome.org /
- https://www.fil.ion.ucl.ac.uk/spm
- http://www.gin.cnrs.fr/en/tools/aal-aal2/
Список литературы
Абрахамс, С., Гольдштейн, Л. Х., Симмонс, А., Браммер, М. Дж., Уильямс, С. К., Джампьетро, В. П. и др. (2003). Функциональная магнитно-резонансная томография беглости речи и называния конфронтации с использованием сжатого изображения для получения явных ответов. Гум. Brain Mapp. 20, 29–40. DOI: 10.1002 / HBM.10126
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Амунц, К., Кедо, О., Киндлер, М., Пиперхофф, П., Мольберг, Х., Шах, Н. Дж. И др. (2005). Цитоархитектоническое картирование миндалевидного тела человека, области гиппокампа и энторинальной коры: карты межпредметной изменчивости и вероятности. Анат. Эмбриол. 210, 343–352. DOI: 10.1007 / s00429-005-0025-5
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Барч Д. М., Берджесс Г. К., Хармс М. П., Петерсен С. Е., Шлаггар Б. Л., Корбетта М. и др. (2013). Функция в коннектоме человека: задача-фМРТ и индивидуальные различия в поведении. Нейроизображение 80, 169–189. DOI: 10.1016 / j.neuroimage.2013.05.033
М., Берджесс Г. К., Хармс М. П., Петерсен С. Е., Шлаггар Б. Л., Корбетта М. и др. (2013). Функция в коннектоме человека: задача-фМРТ и индивидуальные различия в поведении. Нейроизображение 80, 169–189. DOI: 10.1016 / j.neuroimage.2013.05.033
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Бекманн, К. Ф., Дженкинсон, М., и Смит, С. М. (2003). Общее многоуровневое линейное моделирование для группового анализа в FMRI. Нейроизображение 20, 1052–1063. DOI: 10.1016 / S1053-8119 (03) 00435-X
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Беллман, Р. (1961). Процессы адаптивного управления: экскурсия .Принстон, Нью-Джерси: Издательство Принстонского университета. DOI: 10.1515 / 9781400874668
CrossRef Полный текст | Google Scholar
Биндер, Дж. Р., Гросс, У. Л., Аллендорфер, Дж. Б., Бонилья, Л., Чапин, Дж., Эдвардс, Дж. К. и др. (2011). Картирование языковых областей передней височной доли с помощью фМРТ: многоцентровое нормативное исследование. Neuroimage 54, 1465–1475. DOI: 10.1016 / j.neuroimage.2010.09.048
Neuroimage 54, 1465–1475. DOI: 10.1016 / j.neuroimage.2010.09.048
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Браун, С., Мартинес, М. Дж., И Парсонс, Л. М. (2010). Музыка и язык бок о бок в мозгу: ПЭТ-исследование генерации мелодий и предложений. Eur. J. Neurosci. 23, 2791–2803. DOI: 10.1111 / j.1460-9568.2006.04785.x
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Шанель, Г., Пишон, С., Конти, Л., Бертос, С., Шевалье, К., и Грезес, Дж. (2016). Классификация аутичных людей и контрольных групп с использованием кросс-задачной характеристики активности фМРТ. Neuroimage Clin. 10, 78–88. DOI: 10.1016 / j.nicl.2015.11.010
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Черкасский, В. (1997). Природа статистической теории обучения∼. Технометрика 38, 409–409.
Google Scholar
Де, М. Ф., Джентиле, Ф., Эспозито, Ф., Балси, М., Ди, С. Ф., Гебель, Р. и др. (2007). Классификация независимых компонентов фМРТ с использованием отпечатков пальцев IC и вспомогательных векторных машинных классификаторов. Нейроизображение 34, 177–194. DOI: 10.1016 / j.neuroimage.2006.08.041
и др. (2007). Классификация независимых компонентов фМРТ с использованием отпечатков пальцев IC и вспомогательных векторных машинных классификаторов. Нейроизображение 34, 177–194. DOI: 10.1016 / j.neuroimage.2006.08.041
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Де, М. Ф., Валенте, Г., Стаерен, Н., Эшбернер, Дж., Гебель, Р., и Формизано, Э. (2008). Объединение многовариантного выбора вокселей и вспомогательных векторных машин для отображения и классификации пространственных паттернов фМРТ. Нейроизображение 43, 44–58. DOI: 10.1016 / j.neuroimage.2008.06.037
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Эккер, К., Rocharego, V., Johnston, P., Mouraomiranda, J., Marquand, A., Daly, E.M, et al. (2010). Изучение прогностической ценности МРТ структур всего мозга при аутизме: подход к классификации паттернов. Нейроизображение 49:44. DOI: 10.1016 / j.neuroimage.2009.08.024
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Файнберг, Д. А., Мёллер, С., Смит, С. М., Ауэрбах, Э., Раманна, С., Глассер, М. Ф. и др. (2010). Мультиплексная эхо-планарная визуализация для субсекундной FMRI всего мозга и быстрой диффузной визуализации. PLoS One 5: e15710. DOI: 10.1371 / journal.pone.0015710
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Фристон К. Дж., Холмс А. П., Уорсли К. Дж., Полайн Дж. П., Фрит К. Д. и Фраковяк Р. С. Дж. (1994). Статистические параметрические карты в функциональной визуализации: общий линейный подход. Гум. Brain Mapp. 2, 189–210. DOI: 10.1002 / HBM.460020402
CrossRef Полный текст | Google Scholar
Fu, C.H., Mourao-Miranda, J., Costafreda, S. G., Khanna, A., Marquand, A. F., Williams, S. C., et al. (2008). Классификация паттернов грустной обработки лица: к развитию нейробиологических маркеров депрессии. Biol. Психиатрия 63, 656–662. DOI: 10.1016 / j.biopsych.2007.08.020
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Гайдош, М., Микл, М., и Маречек, Р. (2016). Mask_explorer: инструмент для исследования масок мозга в групповом анализе фМРТ. Comput. Методы Прогр.Биомед. 134, 155–163. DOI: 10.1016 / j.cmpb.2016.07.015
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Газзанига М. С., Иври Р. Б., Мангун Г. Р. и Стивен М. С. (2013). Когнитивная нейронаука: биология разума . Нью-Йорк, штат Нью-Йорк: W. W. Norton & Company, Inc.
Google Scholar
Гольдберг, И. И., и Харел, М. Р. (2006). Когда мозг теряет самообладание: префронтальная инактивация во время сенсомоторной обработки. Neuron 50, 329–339. DOI: 10.1016 / j.neuron.2006.03.015
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Гийон, И. (2003). Введение в выбор переменных и функций. J. Mach. Учиться. Res. 3, 1157–1182.
Google Scholar
Хэксби, Дж. В., Гоббини, М. И., Фьюри, М. Л., Ишаи, А., Схоутен, Дж. Л., и Пьетрини, П. (2001). Распределенные и перекрывающиеся изображения лиц и предметов в вентральной височной коре. Наука 293, 2425–2430. DOI: 10.1126 / science.1063736
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Холмс, А. П., и Фристон, К. Дж. (1998). Обобщаемость, случайные эффекты и вывод населения. Нейроизображение 7: S754. DOI: 10.1016 / S1053-8119 (18) 31587-8
CrossRef Полный текст | Google Scholar
Хуанг, Г. Б., Чжоу, Х., Дин, X., и Чжан, Р. (2012). Экстремальная обучающая машина для регрессии и мультиклассовой классификации. IEEE Trans. Syst. Человек Киберн. В 42, 513–529. DOI: 10.1109 / TSMCB.2011.2168604
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Леунг, Х. К., Гор, Дж. К., и Гольдманракич, П. С. (2002). Устойчивая мнемоническая реакция в средней лобной извилине человека во время онлайн-просмотра пространственных меморандумов. J. Cogn. Neurosci. 14, 659–671. DOI: 10.1162 / 089892045882
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Lv, J., Янь, Т., Тао, Л., и Чжао, Л. (2015). Роль конфигурационной обработки в классификации лиц по расе: исследование ERP. Фронт. Гм. Neurosci. 9: 679. DOI: 10.3389 / fnhum.2015.00679
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Майер, Г., Лобергер, А., Бутцен, С., Пофаль, М., Слепой, М., и Хекель, А. (2009). От отбора к аптамеру в клетке: идентификация светозависимых аптамеров оцДНК, нацеленных на цитохезин. Bioorg. Med. Chem. Lett. 19, 6561–6564.DOI: 10.1016 / j.bmcl.2009.10.032
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Мейер, Т. Б., Деспанд, А. С., Вергун, С., Наир, В. А., Сонг, Дж., Бисвал, Б. Б. и др. (2012). Поддержка векторной машинной классификации и характеристики возрастной реорганизации функциональных сетей мозга. Нейроизображение 60, 601–613. DOI: 10.1016 / j.neuroimage.2011.12.052
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Мёллер, С., Yacoub, E., Olman, C.A., Auerbach, E., Strupp, J., Harel, N., et al. (2010). Многополосный мультисрезовый GE-EPI при 7 тесла, с 16-кратным ускорением с использованием частичной параллельной визуализации с применением к высокочастотной пространственной и временной FMRI всего мозга. Magn. Резон. Med. 63, 1144–1153. DOI: 10.1002 / mrm.22361
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Норман К. А., Полин С. М., Детре Г. Дж. И Хаксби Дж. В. (2006). Помимо чтения мыслей: анализ множественных вокселей данных фМРТ. Trends Cogn. Sci. 10, 424–430. DOI: 10.1016 / j.tics.2006.07.005
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Перейра, Ф., Митчелл, Т., и Ботвиник, М. (2009). Классификаторы машинного обучения и фМРТ: обзор учебника. Нейроизображение 45 (1 приложение), S199 – S209. DOI: 10.1016 / j.neuroimage.2008.11.007
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Шёлкопф, Б. (2000). «Уловка ядра для расстояний», в Трудах 13-й Международной конференции по системам обработки нейронной информации, , (Кембридж, Массачусетс: MIT Press), 283–289.
Google Scholar
Спасоевич, Г., Малобабич, С., Пилипович-Спасоевич, О., Джукич-Мацут, Н., и Маликович, А. (2013). Морфология и цифровая морфометрия парацентральной доли человека. Folia Morphol. 72, 10–16. DOI: 10.5603 / FM.2013.0002
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Тиан, Л., Ван, Дж., Ян, К., и Хе, Ю. (2011). Связанные с полушарием и полом различия в мозговых сетях малого мира: функциональное МРТ-исследование в состоянии покоя. Нейроизображение 54, 191–202. DOI: 10.1016 / j.neuroimage.2010.07.066
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Тибширани Р. (1996). Регрессионное сжатие и выбор с помощью лассо. J. R. Stat. Soc. 58, 267–288. DOI: 10.1111 / j.2517-6161.1996.tb02080.x
CrossRef Полный текст | Google Scholar
Тонконоги Дж. И Гудгласс Х. (1981). Языковая функция, ступня третьей лобной извилины и роландическая покрышка. Arch.Neurol. 38, 486–490. DOI: 10.1001 / archneur.1981.00510080048005
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Угурбил К., Сюй, Дж. К., Ауэрбах, Э. Дж., Мёллер, С., Ву, А. Т., Дуарте-Карвахалино, Дж. М. и др. (2013). Повышение пространственного и временного разрешения для функциональной и диффузной МРТ в проекте коннектома человека. Нейроизображение 80, 80–104. DOI: 10.1016 / j.neuroimage.2013.05.012
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Ван, Дж., Ван, X., Ся, М., Ляо, X., Эванс, А., и Хэ, Y. (2015). GRETNA: набор инструментов для сетевого анализа теоретических графов для визуализации коннектомики. Фронт. Гм. Neurosci. 9: 386. DOI: 10.3389 / fnhum.2015.00386
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Wang, L., Wang, W., Yan, T., Song, J., Yang, W., Wang, B., et al. (2017). Функциональная связь в бета-диапазоне влияет на аудиовизуальную интеграцию в пожилом возрасте: исследование ЭЭГ. Фронт. Aging Neurosci. 9: 239.DOI: 10.3389 / fnagi.2017.00239
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Ван, Ю., Лин, Л., Куль, П., и Хирш, Дж. (2007). Математическая и лингвистическая обработка различается между родным и вторым языками: исследование фМРТ. Brain Imaging Behav. 1, 68–82. DOI: 10.1007 / s11682-007-9007-y
CrossRef Полный текст | Google Scholar
Warrier, C., Wong, P., Penhune, V., Zatorre, R., Parrish, T., Abrams, D., et al. (2009). Связь структуры с функцией: извилина Хешля и акустическая обработка. J. Neurosci. 29, 61–69. DOI: 10.1523 / JNEUROSCI.3489-08.2009
CrossRef Полный текст | Google Scholar
У Дж., Янь Т., Чжэнь З., Цзинь Ф. и Го К. (2012). Ретинотопное картирование периферического поля зрения на зрительную кору человека с помощью функциональной магнитно-резонансной томографии. Гум. Brain Mapp. 33, 1727–1740. DOI: 10.1002 / hbm.21324
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Xin, L., Duygu, T., Weiner, M. W., and Norbert, S.(2013). Локально линейное внедрение (LLE) для классификации болезни Альцгеймера на основе МРТ. Neuroimage 83,148–157. DOI: 10.1016 / j.neuroimage.2013.06.033
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Янь Т., Донг X., Му Н., Лю Т., Чен Д., Дэн Л. и др. (2017а). Положительное преимущество классификации: отслеживание хода времени на основе колебаний мозга. Фронт. Гм. Neurosci. 11: 659. DOI: 10.3389 / fnhum.2017.00659
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Ян Т., Фэн, Ю., Лю, Т., Ван, Л., Му, Н., Донг, X., и др. (2017b). Тета-осцилляции, связанные с распознаванием ориентации в автоматическом состоянии: исследование vMMN. Фронт. Behav. Neurosci. 11: 166. DOI: 10.3389 / fnbeh.2017.00166
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Ян Т., Джин Ф., Хе Дж. И Ву Дж. (2011). Разработка системы визуального представления широкого обзора для визуального ретинотопного картирования во время функциональной МРТ. J. Magn. Резон. Imaging 33, 441–447.DOI: 10.1002 / jmri.22404
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Ян, Т., Ван, В., Ян, Л., Чен, К., Чен, Р., и Хан, Ю. (2018). Богатые клубные нарушения коннектома человека от субъективного снижения когнитивных функций до болезни Альцгеймера. Theranostics 8, 3237–3255. DOI: 10.7150 / thno 23772
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Чжан, Дж., Андерсон, Дж. Р., Лян, Л., Пулапура, С. К., Гейтвуд, Л., Роттенберг, Д.A., et al. (2009). Оценка и оптимизация конвейеров обработки отдельных объектов фМРТ с помощью NPAIRS и CVA второго уровня. Magn. Резон. Imaging 27, 264–278. DOI: 10.1016 / j.mri.2008.05.021
PubMed Аннотация | CrossRef Полный текст | Google Scholar
. На законодательном уровне в ст. 13 и 14 Федерального закона от 27.07.2006 № 149-ФЗ «Об информации, информационных технологиях и о защите информации» установить приоритет программного (посредством API) доступа к порталам сдачи отчетности и иным государственным информационным системам, а также заблаговременной публикации любых изменений в формы и форматы предоставления данных в адрес госорганов.
На законодательном уровне в ст. 13 и 14 Федерального закона от 27.07.2006 № 149-ФЗ «Об информации, информационных технологиях и о защите информации» установить приоритет программного (посредством API) доступа к порталам сдачи отчетности и иным государственным информационным системам, а также заблаговременной публикации любых изменений в формы и форматы предоставления данных в адрес госорганов.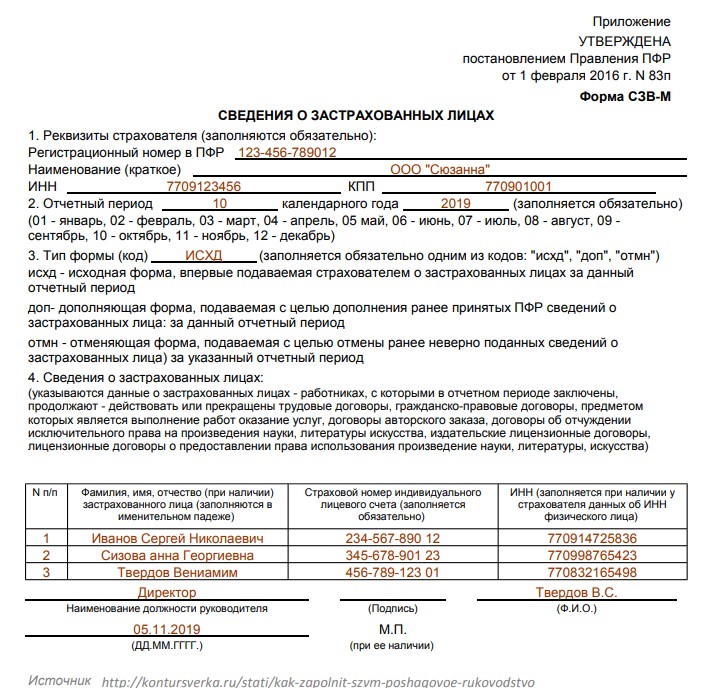 Предлагаем по итогам 2020 года наладить обмен информацией между Росстатом и ФНС России для заполнения формы 12-Ф.
Предлагаем по итогам 2020 года наладить обмен информацией между Росстатом и ФНС России для заполнения формы 12-Ф.



 00
00 92
92 79
79 95
95 99
99 84
84

 images [6], интерполяция = 'ближайший')
images [6], интерполяция = 'ближайший')  Библиотеки Python для анализа данных и машинного обучения
Библиотеки Python для анализа данных и машинного обучения Вопросы и ответы на собеседовании по Django
Вопросы и ответы на собеседовании по Django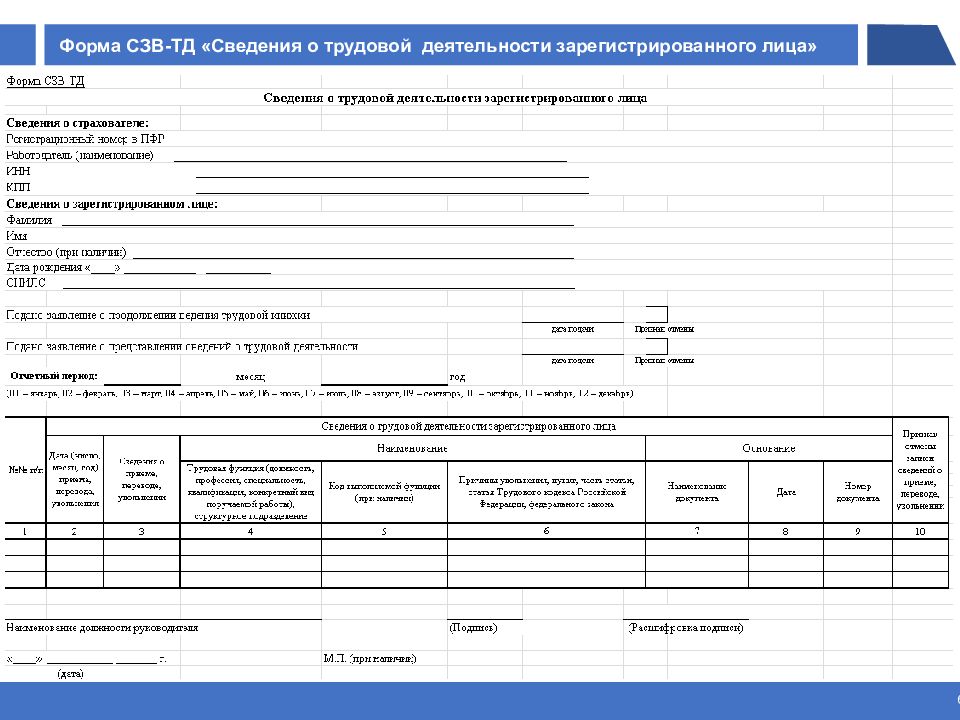 3, random_state = 0)
print ('Обучающий набор содержит {} образцов, а тестовый набор содержит {} образцы'.format (X_train.shape [0], X_test.shape [0]))
3, random_state = 0)
print ('Обучающий набор содержит {} образцов, а тестовый набор содержит {} образцы'.format (X_train.shape [0], X_test.shape [0])) 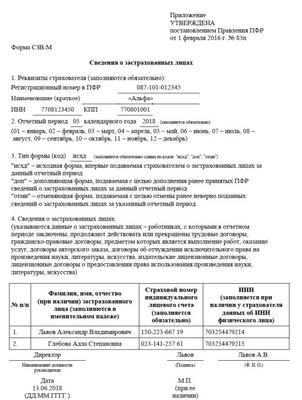 fit (X_train)
X_train_standard = standard_scaler.transform (X_train)
X_test_standard = standard_scaler.transform (X_test)
print ('Первые пять строк после стандартизации выглядят так: \ n')
print (pd.DataFrame (X_train_standard, columns = iris_dataframe.columns) .head ())
fit (X_train)
X_train_standard = standard_scaler.transform (X_train)
X_test_standard = standard_scaler.transform (X_test)
print ('Первые пять строк после стандартизации выглядят так: \ n')
print (pd.DataFrame (X_train_standard, columns = iris_dataframe.columns) .head ()) 
